Тема дипломного проекта — математическое моделирование социально-психологических проблем

метки: Семья, Модель, Женщина, Моделирование, Объект, Профсоюз, Развитие, Управление

MINISTRY OF EDUCATION AND SCIENCE OF THE REPUBLIC OF KAZAKHSTAN

INTERNATIONAL INFORMATION TECHNOLOGY UNIVERSITY JSC

FACULTY OF INFORMATION TECHNOLOGY

Department of Computer Science, Software Engineering and Telecommunication

Major 5B070400 – Computer Science and Software Engineering

APPROVED

Head of the Department,

Dr.Sc.Eng., Professor

___________ «_____» ___________201_

DIPLOMA PROJECT ASSIGNMENT

______ ___Shokanov Asanali_______________________________________

(student name)

1. Diploma project topic

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Approved by IITU order № 56/1 dated «____» _______________ 201

2. Assignment submission deadline ________________________________________________

3. Initial data ___________________________________________________________________

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4. List of issues to be developed _______________________________________________________________________________

______________________________________________________________________________________________________________________________________________________________

5. Laser disc containing the diploma paper text with attachments ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

6. Project consultants, by sections Section	Consultant		Signature, date
Assigned by		Received by

Date of issuing the assignment ______________________________________________

Supervisor_______________________________________________________________

(signature)

Received by______________________________________________________________

(signature)

Аннотация

Тема дипломного проекта — математическое моделирование социально-психологических проблем

Цель проекта — рассмотреть ряд социально-психологических проблем общества, и построить определенную математическую модель, позволяющую сделать прогнозы, выявить действующий статус проблемы. Провести исследование относительно одной среднестатистической семьи во время экономического кризиса, сделать анализ последующей обстановки после выполнений определенных условий.

Согласно принятым требованиям, дипломный проект состоит из 4 глав: аналитическая часть, проектирование и программная реализация, охрана труда и промышленная экология, обоснование экономической эффективности проекта. А также дипломный проект содержит: аннотацию, содержание, введение, заключение, список использованной литературы и приложения.

Abstract

The theme of the graduation project — mathematical modeling of social and psychological problems

The purpose of the project — to consider a number of socio-psychological problems of society, and to build a specific mathematical model to make predictions , to identify the current status of the problem. Conduct research on one of the average family during the economic crisis, making the subsequent analysis of the situation after the fulfillment of certain conditions.

According to the accepted requirements, thesis project consists of four chapters: the formulation of the problem, the design and software implementation, labor protection and industrial ecology, the rationale of economic efficiency of the project. A thesis project also contains a short abstract, contents, introduction, conclusion, bibliography and appendices.

Введение

1. Глава 1. Аналитическая часть.

Общие положения теории моделирования

1. 1. Моделирование как метод исследования сложных систем
   2. Классификация моделей
   3. Основные этапы математического моделирования
   4. Математическое Моделирование и всеобщая компьютеризация или имитационные модели
2. Глава 2. Практическая часть. Моделирование семьи

2.1.2 Реализация модели

2.1.3 Компьютерный эксперимент

2.2 Модель “хищник-жертва”

2.3 Модель “Семейная История”

2.4 Исследование математической модели на устойчивость

2.5 Модель “Профсоюзная деятельность”

2. Глава 3.Экономическая часть

4. Глава 4.Обж

Заключение

Использованная литература

Введение

Иллюстрацией и подтверждением исследований, содержащихся в этой дипломной работе, может служить статья известного американского социолога Роберта Макгиннса «Новое в методах исследования». Статья вышла в 1968 году в известном сборнике «American Sociology: Perspectives, Problems, Methods» под редакцией Т.Парсонса. Макгиннис предупреждал о надвигающейся революции социологии относительно математической науки; грядущих радикальных событиях, которые скоро принесут как большие достижения? Так и серьезные потери.

Он писал: «Несмотря на отсутствие математики можно даже сказать отвращение к ней – в традиционных аспирантских программах, некоторые социологи начинают открывать ее для ссебя как потенциальный язык теории. Их привлекает надежда, возможно, даже обещание, которое сулит математика относительно улучшения социологической теории…»

Свидетельством революции в методах является по Р.Макгиннису не только обращение к языку математики, но и использование компьютеров. Автор (как и многие его современники) пишет, что компьютер в социологии это не только сверхскоростной арифмометр.

В классической работе Жана-Франсуа Лиотара «Состояние постмодерна» информатизация общества связывается с возникновением особого постмодернистского видения мира. Французский философ отмечает, что «при таком всеобщем изменении природа знания не может оставаться неизменной». Распространение информационных технологий неминуемо изменяет статус и характер научного знания. В чем же выражается это изменение?

Ответ простой, изменения выражаются в имитации реальности, а именно в имитации социума.

Для современной науки характерным является то, что материальный эксперимент все чаще заменяется экспериментом на моделях. «Если раньше теории могли строиться только на основе некоего порядка, присущего вещям, то теперь вполне допустимо моделирование без выхода к каким-либо реальным референтам, например, компьютерные симуляции природных, технологических и социальных процессов».

Современный исследователь погружается в виртуальную реальность симуляций, строя искусственное общество искусственных людей. Заимствуя схему определения универсальных свойств виртуальной реальности, рассмотрим замысел компьютерного моделирования.

Несомненно, компьютерное моделирование является вариантом киберпротезирования реального общества. От реального общества автор модели переходит к его протезу «искусственному обществу». При этом исследователю приходится ограничивать разнообразие вариантов, отбрасывая некоторые признаки и упрощая другие.

Компьютерное моделирование – типичная область знания, обладающая специфической «постмодернистской чувственностью» — особым, плюралистичным отношением к миру, избегающем излишнего обобщения и диктата тоталитаризирующих истин. Порожденное постмодернистским информационным обществом, оно также предполагает отсутствие инвариантных базисных истин для объектов различных классов. Данный вид моделирование «открыт» самым разнообразным социологическим теориям. Используя реалистичные теоретические схемы и модели, исследователь погружается в плодотворную и захватывающую работу.

В то же время, моделируя общество, компьютеры являются уникальным инструментом порождения теории. Известно, что компьютерные эксперименты весьма перспективны для разработки социологических теорий, благодаря которым можно обобщить крупные массивы имеющихся данных и с большей целенаправленностью организовать процесс эмпирического исследования.

Однако, как у любого метода, у компьютерного моделирования достаточно спорных идей и иллюзий. Мы не будем подробно обсуждать здесь доводы, проводимые противниками количественных методов в социологии относительно математики. Суть западни, в которую попадают социологи, использующие компьютерное моделирование, заключается в природе математического языка. Как писал известный Роберт Макгиннис: «Математика – это язык, который богат, но не двусмыслен, скуп, но не догматичен. Современный разговорный язык, даже обильно сдобренный социологически жаргоном, страдает в этом отношении(то есть как орудие теории) серьезными недостатками ».

Уже несколько лет с развитием вычислительной техники появилась возможность решать инженерно-геометрические задачи путем численного моделирования. В памяти компьютера создаются на цифровой основе геометрические объекты и геометрические отношения, адекватные реальным, а решение сводиться к численному оперированию с информационными, или, как принято говорить, математическими моделями.

Особенностью современного этапа развития техники является качественно новый подход к проектированию и разработке новых видов изделий, базирующийся на принципе оптимизации параметров изделия на этапе предварительного проектирования. Глубокий и всесторонний анализ решений, принимаемых на стадии проектирования, позволяет существенно снизить сроки и затраты на проведение испытаний, доводку и внедрение изделия в серийное производство. Сокращение сроков разработки новых образцов и ускорение научно-технического прогресса невозможны без самого широкого внедрения вычислительной техники в процесс проектирования.

С точки зрения социологии моделирование – эффективное средство познания природы. Процесс моделирования предполагает наличие:

— объекта исследования;

— исследователя, перед которым поставлена конкретная задача;

— модели, создаваемой для получения информации об объекте и необходимой для решения поставленной задачи.

Вычислительный эксперимент – переход от изучения реального объекта к изучению его математической модели.

Преимуществами вычислительного эксперимента являются:

— возможность исследования объекта без модификации установки или аппарата;

— возможность исследования каждого фактора в отдельности, в то

время как в реальности они действуют одновременно;

— возможность исследования нереализуемых на практике процессов.

Вычислительный эксперимент включает в себя следующие этапы:

— физическое описание процесса, то есть уяснение закономерности протекаемых явлений.

— разработка математической модели.

— алгоритм или метод решения уравнений.

— разработка программ.

— проведение расчетов, анализ результатов и оптимизация.

Данный дипломный проект написан учитывая все вышеизложенные теории и высказывания. Рассматриваются актуальные социально-психологические проблемы общества.

Цель исследования :рассмотреть ряд социально-психологических проблем общества, и построить определенную компьютерную модель, позволяющую сделать прогнозы, выявить действующее положение проблемы.

Задачи исследования:

1. выявить самые актуальные социальные проблемы.
2. Построить математическую модель каждой из проблем.
3. На основе математической модели проделать компьютерное моделирование (написать программный код), позволяющий выявить определенные графики, диаграммы.
4. На основе выявленных графиков и диаграмм, проделать определенные прогнозы и анализы

Объектом исследования является действующие отношения на примере одной семьи; кризисная обстановка в профсоюзной деятельности

Предметом исследования является математическое и компьютерное моделирование профсоюзной деятельности одной фирмы, математической моделирование и прогнозы развития отношении в одной семье.

Глава 1.Аналитическая часть

Общие положения теории моделирования

Под моделированием в широком смысле понимают не только процесс построения, изучения и совершенствования моделей, но и использование их в научных исследованиях, в том числе и экспериментальных, а также применение их непосредственно в процессах планирования, управления,

прогнозирования, контроля и т.д.

Моделирование как метод исследования является мощным инструментом познания на протяжении всей истории развития человечества. Одним из примеров созданной человеком системы моделей, адекватно отражающей широкий класс явлений и процессов реального мира, являются модели классической механики.

Моделирование как инструмент познания требует творческого подхода и определенного искусства владения им. С другой стороны, моделирование как наука опирается на научные знания той области, где этот инструмент познания используется. Например, для построения математической модели летательного аппарата (ЛА) требуются знания законов аэродинамики, механики, движения ЛА в воздушной и безвоздушной среде. Только глубокие профессиональные знания исследователя в сочетании с творческим подходом к решаемой проблеме могут быть основой для успешного применения метода моделирования. Сам процесс моделирования предполагает такой способ изучения объекта, при котором модель, с точки зрения цели исследования, вполне точно (адекватно) и достаточно полно замещает изучаемый объект.

Существует достаточно большое число определений понятия «модель». Одни из них слишком абстрактны, другие — слишком конкретны. Все они отражают ту или иную сторону этого многогранного понятия.

Модель — это вспомогательный объект (устройство, средство), который может заменить другой объект.

Модель — это упрощенное представление другого объекта или процесса.

Модель — это форма представления и существования наших знаний.

Модель — это инструмент познания окружающего мира.

В дальнейшем будем придерживаться следующего определения понятия модели, которое; является более узким и более конкретным .

Определение 1. Объект М является в определенных условиях моделью системы (объекта, процесса, явления, ситуации) S относительно некоторого множества С, его характеристик (свойств, признаков), если М строится для имитации S по этим характеристикам.

Таким образом, модель и исходная система эквивалентны относительно множества воспроизводимых характеристик:

При этом следует иметь в виду, что модель М по сравнению с оригиналом S имеет существенные преимущества: наглядность, простоту, обозримость, легкость преобразований с ней, возможность проведения испытаний и получения с ее помощью новых знаний, информации.

Само понятие модели претерпевало так же, как и понятие системы, определенную эволюцию. Эволюция моделей отражает эволюцию процесса познания.

Так, на ранних этапах под моделью понимали некоторое физическое устройство (объект), которое в определенных условиях заменяет другой объект. Примерами таких устройств могут служить модели самолетов, кораблей, машин, различные макеты, шаблоны, протезы и т.д.

На следующем этапе под моделью объекта понимался объект-заменитель, который отражал лишь интересующие исследователя свойства и характеристики объекта-оригинала. При этом модель перед объектом обладал такими преимуществами, как наглядность, простота, обозримость, доступность для эксперимента, возможность идентификации и т.д. Само понятие модели уже значительно расширено и включает в себя чертежи, таблицы, характеристики, графики, рисунки, картографические изображения, различные формы описания устройств и т.д.

На третьем же этапе в понятие модели включают на только реальные (физические, материальные), но и абстрактные (идеальные) построения. Примером последних могут служить идеи, гипотезы, теории, математические, логические и имитационные модели. В форме математической модели можно описать и типовую деятельность человека-оператора в организационно-технических системах. Сам процесс мышления можно трактовать как процесс последовательного перехода от одних абстрактных моделей к другим. При этом модель выступает как форма существования и представления знаний об исследуемом объекте, явлении, процессе, системе. Таким образом, познание материального мира идет через модели, а целенаправленная деятельность человека невозможна без моделирования.

Укажем и на другие свойства моделей. Во-первых, модель очень информативна, а эта информация представлена в весьма сжатом виде. Во-вторых, модель иерархична, т.е. есть модели более высокого уровня (например, модель системы управления) и более низкого (например, модели элементов систем управления).

В-третьих, модель уточняется и корректируется в процессе моделирования, т.е. недостатки модели нельзя предугадать заранее. В-четвертых, модель может выступать в качестве эталона, идеализирующего собой различные формы деятельности: управление, планирование, принятие решений, прогнозирование, контроль и т.д. Например, в адаптивных системах управления техническими объектами реализуется принцип управления по эталонной модели. С этой точки зрения цель системы управления часто выступает в качестве модели будущего (желаемого) состояния системы. А алгоритм можно рассматривать как модель формирования управляющих воздействий, направленных на перевод объекта управления из одного состояния в другое. При этом модель привода рассматривается как модель исполнения управляющих воздействий путем перемещения органов регулирования, а модель информационных элементов (датчиков) — как модель обработки и преобразования первичной информации. Таким образом, исследование системы управления происходит через построение моделей ее элементов и изучение свойств системы путем моделирования ее поведения в различных условиях.

Необходимо помнить и о главном недостатке метода моделирования, который заключается в том, что при моделировании можно получить результаты, не имеющие отношения к исследуемым свойствам системы или неправильно отражающие свойства реальной системы. В этом есть объективная причина: модель не всегда точно и достаточно полно отражает реальный объект. Но все же достоинств у метода моделирования больше, чем недостатков.

Можно выделить следующие достоинства:

1. Модели практичны, они всегда строятся так, чтобы были проще и удобнее для исследований, чем исходные объекты. На моделях можно ставить такие эксперименты, проведение которых на реальных объектах либо слишком дорого, либо опасно для персонала и окружающей среды. Например, на моделях системы управления авиационным двигателем можно изучать ее свойства на различных скоростях и высотах полета Л A вместо изучения этих свойств на дорогостоящих высотных стендах.

2. Некоторые явления можно изучать только на их моделях. Например, ядерные взрывы, электрические разряды молнии, полет JIA при развитии критической ситуации на борту в результате отказов отдельных функциональных подсистем, возникновения пожара и т.п.

3. Модели воспроизводят лишь основные, наиболее важные для данного исследования свойства изучаемой системы. Это позволяет при моделировании выявить механизм формирования данных свойств системы, научиться прогнозировать эти свойства и целенаправленно их изменять в желаемую сторону.

4. При моделировании систем могут возникнуть и побочные эффекты. Например, модель может воспроизводить такие свойства системы, которые адекватны реальным, но данная модель не была предназначена для этого. Этот эффект следует рассматривать как исключение, а не как закономерность. Указанные достоинства метода моделирования делают его наиболее эффективным методом, как научных исследований, так и практической деятельности человека.

1.2. Классификация моделей

Проблема классификации моделей, как и любых достаточно сложных явлений, процессов, систем, сложна, многогранна и трудноразрешима. Объективная причина состоит в том, что исследователя интересует лишь какое-то одно свойство системы (объекта, процесса, явления), для отображения которого и создана модель. Поэтому в основу классификации можно положить множество различных признаков: способ описания, функциональное назначение, степень детализации, структурные свойства, область применения и т.д.

Рассмотрим некоторые классы моделей.

1. По назначению моделей различают:

• исследовательские (познавательные, когнитивные), предназначенные для генерации знаний путем изучения свойств объекта;

• учебные, предназначенные для передачи знаний об изучаемом объекте;

• рабочие (прагматические), предназначенные для генерации правильных действий в процессе достижения цели.

К исследовательским моделям относятся полунатурные стенды, физические модели, математические модели. Отметим, что исследовательские модели могут выступать в качестве учебных, если они предназначены для передачи знаний о свойствах объекта. Примерами рабочих моделей могут служить: робот; автопилот; математическая модель объекта, встроенная в систему управления или контроля; искусственное сердце и т.д. При этом исследовательские и учебные модели должны приближаться к реальности, а рабочие модели должны отражать эту реальность. Четкой границы между этими моделями не существует. Так, например, исследовательская модель, адекватно отражающая свойства объекта, может быть использована в качестве рабочей. Исследовательские модели являются носителями новых знаний, учебные модели соединяют старые знания с новыми. Рабочие модели идеализируют накопленные знания в форме идеальных действий по выполнению тех или иных функций, которые желательно было бы осуществить.

2. По отражению режимов работы системы различают:

•. статические модели, которые отражают установившиеся (равновесные) режимы работы системы;

• динамические, которые отражают неустановившиеся (неравновесные, переходные) режимы работы системы.

Статические режимы работы элементов, объектов, систем отражены в их статических характеристиках (линейных, нелинейных) и описываются соответствующими алгебраическими функциональными зависимостями.

3. По способу создания (построения) моделей различают:

• абстрактные (дедуктивные, умозрительные, идеальные) модели, построенные средствами мышления на базе нашего сознания;

• материальные (физические, реальные) модели, построенные средствами материального мира для отражения его объектов, процессов и т.д.

Абстрактные модели — это идеальные конструкции в нашем сознании в виде образов или представлений о тех или иных физических явлениях, процессах, ситуациях, объектах, системах. Примерами абстрактных моделей могут служить какая-либо гипотеза о свойствах материи, предположения о поведении сложной системы в условиях неопределенности или новая теория о строении сложных систем. На абстрактных моделях и на умозрительной аналогии (сходстве) между моделью М и оригиналом S строится идеальное (дедуктивное) моделирование. Различают два вида идеального моделирования: формализованное и неформализованное (интуитивное).

К формализуемым абстрактным моделям относятся знаковые модели, в том числе математические и языковые конструкции (языки программирования, естественные языки) вместе с правилами их преобразования и интерпретации. Примером знаковых моделей могут служить чертежи, схемы, графики, формулы и т.д. Математическое моделирование — частный случай знакового моделирования. Здесь преобразование формул осуществляется на основе правил логики и математики.

Математическая модель — это объект, который имеет с прототипом следующее однозначное соответствие: 1) структуры, т.е. состава элементов и связей между ними; 2) уравнений, описывающих свойства этих элементов и их связей. При этом математическую модель сложной системы можно трактовать как множество математических моделей элементов, взаимосвязанных и взаимодействующих друг с другом и адекватно отражающих синергетические свойства системы.

При образном моделировании модели строятся из каких-либо наглядных элементов (упругие шары, потоки жидкости, траектории движения тел и т.д.).

Анализ образных моделей осуществляется мысленно и может быть отнесен к формализованному моделированию в том случае, когда правила взаимодействия образов четко формализованы. Этот вид моделирования используется при мысленном эксперименте.

Данный дипломный проект представляет собой попытку познакомить социологов с математическим аппаратом и с современными методами решения социологических задач. Вот неполный перечень таких задач:

• обработка и анализ данных опросов и других социологических исследований

• построение математических моделей социальных процессов и явлений

• объяснение и предсказание социальных явлений

Математическое моделирование состоит в замене реального объекта его математической моделью с последующим изучением последней. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.

Многомерное шкалирование – математический инструментарий, предназначенный для обработки данных о отношениях между исследуемыми объектами с целью представления этих объектов в виде точек некоторого пространства восприятия. Этот метод позволяет выявить и интерпретировать латентные (т.е. скрытые и непосредственно не наблюдаемые) признаки, объясняющие связей между исследуемыми объектами. В пособии в качестве метода многомерного шкалирования рассмотрен метрический метод Торгерсона.

Другая задача обработки данных состоит в уменьшении размерность данных, потеряв наименьшее количество информации. Это позволяет, во-первых избавиться от “шума”, т.е. части данных, которая содержит не полезную информацию, а погрешности и ошибки. Во-вторых, чем меньше размерность данных, тем легче их дальнейшее изучение и интерпретация. В качестве аппарата уменьшения размерности данных в пособии рассмотрен метод главных компонент.

Все процессы, развивающиеся во времени и имеющую в причинно-следственную связь моделируются с помощью дифференциальных уравнений (в случае, когда система описывается одной характеристикой) и систем дифференциальных уравнений (когда таких характеристик несколько).

В качестве примера моделирования таких процессов в пособии рассмотрены несколько примеров роста численности популяции некоторой замкнутой экосистемы.

1.3 Основные этапы математического моделирования

1) Построение модели. На этом этапе задается некоторый «нематематический» объект — явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.

2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.

5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

Требования, предъявляемые к моделям.

1. Универсальность — характеризует полноту отображения моделью изучаемых свойств реального объекта.

2. Адекватность — способность отражать нужные свойства объекта с погрешностью не выше заданной.

3. Точность — оценивается степенью совпадения значений характеристик реального объекта и значения этих характеристик полученных с помощью моделей.

4. Экономичность — определяется затратами ресурсов ЭВМ памяти и времени на ее реализацию и эксплуатацию.

1.4 Математическое Моделирование и всеобщая компьютеризация или имитационные модели

Сейчас, когда в стране происходит чуть ли не всеобщая компьютеризация, от специалистов различных профессий приходится слышать высказывания: «Вот внедрим у себя ЭВМ, тогда все задачи сразу же будут решены». Эта точка зрения совершенно не верна, сами по себе ЭВМ без математических моделей тех или иных процессов ничего сделать не смогут и о всеобщей компьютеризации можно лишь мечтать.

В подтверждение вышесказанного попытаемся обосновать необходимость моделирования, в том числе математического, раскроем его преимущества в познании и преобразовании человеком внешнего мира, выявим существующие недостатки и пойдем… к имитационному моделированию, т.е. моделированию с использованием ЭВМ. Но все по порядку.

Прежде всего, ответим на вопрос: что такое модель?

Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.

Хорошо построенная модель доступнее для исследования – нежели реальный объект. Например, недопустимы эксперименты с экономикой страны в познавательных целях, здесь без модели не обойтись.

Резюмируя сказанное можно ответить на вопрос: для чего нужны модели? Для того, чтобы понять, как устроен объект (его структура, свойства, законы развития, взаимодействия с окружающим миром).

Научиться управлять объектом (процессом) и определять наилучшие стратегии прогнозировать последствия воздействия на объект.

Что положительного в любой модели? Она позволяет получить новые знания об объекте, но, к сожалению, в той или иной степени не полна.

Модель сформулированная на языке математики с использованием математических методов называется математической моделью.

Исходным пунктом ее построения обычно является некоторая задача, например экономическая. Широко распространены, как дескриптивные, так и оптимизационные математические, характеризующие различные экономические процессы и явления, например:

распределение ресурсов

рациональный раскрой

транспортные перевозки

укрупнение предприятий

сетевое планирование.

Каким образом происходит построение математической модели?

Во–первых, формулируется цель и предмет исследования.

Во–вторых, выделяются наиболее важные характеристики, соответствующие данной цели.

В–третьих, словесно описываются взаимосвязи между элементами модели. Далее взаимосвязь формализуется. И производится расчет по математической модели и анализ полученного решения.

Используя данный алгоритм можно решить любую оптимизационную задачу, в том числе и многокритериальную, т.е. ту в которой преследуется не одна, а несколько целей, в том числе противоречивых.

Приведем пример. Теория массового обслуживания – проблема образования очередей. Нужно уравновесить два фактора – затраты на содержание обслуживающих устройств и затраты на пребывание в очереди. Построив формальное описание модели производят расчеты, используя аналитические и вычислительные методы. Если модель хороша, то ответы найденные с ее помощью адекватны моделирующей системе, если плоха, то подлежит улучшению и замене. Критерием адекватности служит практика.

Оптимизационные модели, в том числе многокритериальные, имеют общее свойство– известна цель(или несколько целей) для достижения которой часто приходится иметь дело со сложными системами, где речь идет не столько о решении оптимизационных задач, сколько об исследовании и прогнозировании состояний в зависимости от избираемых стратегий управления. И здесь мы сталкиваемся с трудностями реализации прежнего плана. Они состоят в следующем:

1. сложная система содержит много связей между элементами
2. реальная система подвергается влиянию случайных факторов, учет их аналитическим путем невозможен
3. возможность сопоставления оригинала с моделью существует лишь в начале и после применения математического аппарата, т.к. промежуточные результаты могут не иметь аналогов в реальной системе.

В связи с перечисленными трудностями, возникающими при изучении сложных систем, практика потребовала более гибкий метод, и он появился – имитационное моделирование «Simujation modeling».

Обычно под имитационной моделью понимается комплекс программ для ЭВМ, описывающий функционирование отдельных блоков систем и правил взаимодействия между ними. Использование случайных величин делает необходимым многократное проведение экспериментов с имитационной системой (на ЭВМ) и последующий статистический анализ полученных результатов. Весьма распространенным примером использования имитационных моделей является решение задачи массового обслуживания методом МОНТЕ–КАРЛО.

Таким образом, работа с имитационной системой представляет собой эксперимент, осуществляемый на ЭВМ. В чем же заключаются преимущества?

–Большая близость к реальной системе, чем у математических моделей;

–Блочный принцип дает возможность верифицировать каждый блок до его включения в общую систему;

–Использование зависимостей более сложного характера, не описываемых простыми математическими соотношениями.

Перечисленные достоинства определяют недостатки

–построить имитационную модель дольше, труднее и дороже;

–для работы с имитационной системой необходимо наличие подходящей по классу ЭВМ;

–взаимодействие пользователя и имитационной модели (интерфейс) должно быть не слишком сложным, удобным и хорошо известным;

–построение имитационной модели требует более глубокого изучения реального процесса, нежели математическое моделирование.

Встает вопрос: может ли имитационное моделирование заменить методы оптимизации? Нет, но удобно дополняет их. Имитационная модель – это программа, реализующая некоторый алгоритм, для оптимизации управления которым прежде решается оптимизационная задача.

Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человека.

Глава 2.Практическая часть

Моделирование семьи

в социологическом исследовании актуальным вопросом является изучение семьи и гендерных отношений как объектов моделирования. Но социологи не обращают достаточного внимания на формализацию и вычисление многообразных переменных адаптивного гендерного поведения. И это серьезное упущение при поиске ответов на многочисленные вопросы. Как семьи могут становиться стабильными и выживать в ситуации кризиса? Как экономическая трансформация воздействует на женщин в социальной системе? Какие адаптивные действия должны вести к поддержанию стабильности семьи? Как адаптивные способности определяют гендерной согласованностью и персональной активностью женщин?

Желательно создать имитационную мульти-агентную модель, с помощью которой можно будет не только исследовать различные типы адаптивного поведения и само идентичности женщин и мужчин в ситуации экономического кризиса, но и посредством анализа гендерных ролей изучить изменение самоидентичности женщин и ролей мужчин в браке.

Первая цель нашего исследования заключается в том, чтобы продемонстрировать, как могут быть изучены с помощью мульти-агентного моделирования устойчивость и адаптивное поведение семьи.

Вторая цель – проверить следующие гипотезы:

1. стабильность и адаптивное поведение семей в течение экономического кризиса связаны с разнообразными формами индивидуального и совместного действий, например с персональной активности членов семьи и совместимостью гендерных ролей;
2. баланс и согласованность гендерных ролей(ожидаемое поведение индивида в зависимости от его гендера, т.е. от его пола ), профессиональная ориентация и активность женщин определяются высокой адаптивной способностью и устойчивостью семьи.

Сравнение поведения женщин в различных ситуациях позволит выявить типы их поведения, влияющие на выбор того или иного действия, направленного на сохранение семьи.

Имитация различных условий и факторов воздействия на семью очень полезна для анализа стабильности семьи. В этой главе мы познакомимся с моделью адаптивного поведения семьи в условиях экономически неустойчивого общества. С ее помощью возможны:

1. изучение поведения женщин и мужчин в условиях экономической нестабильности;
2. проведение оценок результатов адаптивного выбора;
3. имитация и анализ большого числа различных ситуаций;
4. проведение многочисленных экспериментов.

2.1.1. Модель адаптивного поведения семьи. Формализация семьи

Понятие «семейная стратегия» акцентирует внимание на механизмах формирования и воспроизводства поведения семьи в различных сферах жизнедеятельности и различных ситуациях. Так, выделяют стратегии семьи в осуществлений хозяйственной, репродуктивной и культурной функции; стратегии, направленные на преодоление кризиса, как внешнего по отношению к семье ( например, экономического, социально-культурного), так и внутри-семейного ( например, связанного с переходом на новый этап жизненного цикла семьи или с кризисом внутрисемейных отношений).

Различают также стратегии, характерные для семей с одним и двумя работающими супругами, для неполной семьи, для смей, принадлежащих к разным социальным группам. В предлагаемой модели проблемы семьи связаны материально нестабильности семьи и переживанием постоянной стрессовой ситуации.

Каковы факторы адаптивного поведения и устойчивости семьи? Для того чтобы ответить на этот вопрос нужно определить идентичность и интересы членов семьи. На основании указанных признаков будем в модели разбивать агентов на различные группы.

Первая группа агентов состоит из женщин, которые имеют профессиональную ориентацию. Вторая группа агентов состоит из женщин с ориентацией на семейную жизнь. Современная казахстанская гендерная система демонстрирует корреляцию между профессиональной ориентацией и успешным адаптивным экономическим поведением семьи. Многие семьи, женщины в которых заняты своей карьерой, экономически и социально более преуспевают, чем семьи с семейной ориентацией женщин. Возрастающее же распространение семей, поддержанных женской профессиональной ориентацией, обусловлено персональной активностью женщин. Третьей группой агентов являются женщины с высокой творческой энергией и адаптивными способностями. Напротив, четвертая группа включает женщин с низкой адаптивной способностью и социальной незащищенностью.

По данным социологического исследования дляя большинства казахстанских мужчин основными источниками идентичности служит работа. В период экономического кризиса и роста профессиональной активности женщин важным фактором является гармония и баланс гендерных ролей. Вот почему в модели полагается, что агенты-мужчины имеют профессиональную идентичностью и высокий уровень толерантности к профессиональной активности женщин.

В ситуации экономического кризиса идет перестройка образа жизни семьи, связанная с адаптацией к реалиям рыночного, нестабильного общества. Мы считаем, что главной семейной стратегией в период экономического кризиса является стратегия выживания. Она осуществляется в разных формах, но основным является семейно-ориентированный образ жизни, предполагающий принятие как мужчинами, так и женщинами традиционных ролей. Вместе с тем, в данном исследовании ставится задача выяснить, какие стратегии адаптивного поведения избирают семьи с целью преодоления социально-экономического кризиса. Если семья выбирает неподходящую для себя стратегию, она лишь какое-то время преодолевает трудности, порожденные экономическим кризисом, однако он неминуемо вновь обрушивается на нее с новой силой. Важно понять, каким образом мужчины и женщины, имеющие определенные гендерные роли, приспосабливаются к условиям жизни в кризисном обществе. Что способствует успеху одних и препятствует адаптации других?

Бюджет семьи, в общем случае, складывается из зарплаты мужа и жены. При этом выделяются «бедные» семьи, с доходом ниже прожиточного минимума, и «состоятельные» с доходом, превышающем прожиточный минимум. Причем семья с относительно высоким общесемейным доходом «задается», главным образом, заработками мужей. Для каждой семьи в модели устанавливаются собственные размеры доходов мужчины и женщины и расхода семьи.

2.1.2 Реализация модели

рассмотрим N семей, состоящих из женщины и постоянно работающего мужчины и обладающих следующими характеристиками:

наличный капитал к-ой семьи в момент времени

начальный уровень адаптации -ой семьи;

начальный уровень толерантности -ой семьи;

степень идентичности женщины в -ой семье в момент времени определим функцией

Динамику изменения капитала опишем следующей разностной задачей

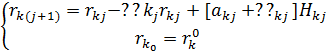(7.1)

вторая часть уравнения (7.1) выражает соответственно расход и общий доход семьи, где

функция дохода мужчины в -ой семье;

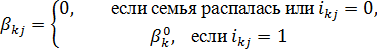
функция дохода женщины.

-ой семьи.

Функция выражает количество ресурса в источнике дохода в момент времени Динамику изменения ресурса зададим следующим уравнением

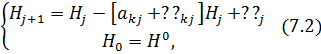
где -прирост/убыль ресурса в источнике с определенной периодичностью. В период экономического кризиса ( происходит уменьшение ресурса в источнике дохода. Во время стабильного экономического развития ( ресурс в источнике постепенно увеличивается.

Опишем правила оценки ситуации и выбора семьей той или иной стратегии адаптивного поведения. Зададим кризисные границы адаптивности и толерантности для семьи: где максимально заданный уровень адаптации семьи, const – максимально заданный уровень толерантности семьи. Пусть максимально заданный уровень капитала семьи, а = const заданная граница экономического кризиса семьи. Оценка ситуации и выбор стратегии поведения определяются с помощью величины следующим образом:

1. если 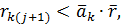то констатируется, что 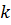-ая семья находится в поисках более богатого источника дохода и

2. если 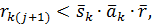тогда констатируется, что семья живет не по средствам, и принимается решение об уменьшение расходов, т.е.

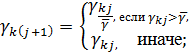
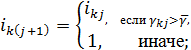
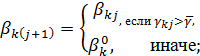
где минимальный уровень расхода.

3. Если 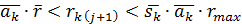, то семья живет в достатке и нет необходимости в изменениях:

4. Если 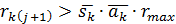, тогда

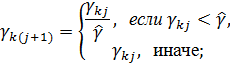
где средний уровень расхода.

5. если 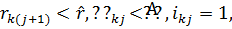где 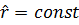граница острого кризиса для семьи, ир происходит распад к-ой семьи, 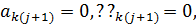и вычисления с помощью уравнения (7.1) дальше не производятся.

Условие (1) означает, что семьи с более высокой адаптацией ощутили происходящие изменения в экономике заблаговременно, до наступления острого кризиса, и успевают сориентироваться. Таким образом, выбирается стратегия поиска более денежной работы.

Условие (2) характеризует стратегия снижения расходов, когда еще не достигнут самый нижний уровень жизнеобеспечения. Другими словами, семья выбирает тип поведения «перекрутимя, будем экономить на всем». Если все же снизить расходы невозможно, то при достаточном уровне толерантности в семье женщина должна будет искать работу.

Условие (3) предполагает выбор выжидательной стратегии адаптивного поведения. Капитал достаточно большой и семья выбирает тип поведения «будем жить как раньше; нам пока хватает».

Условие (4).

Семья живет с доходом, превышающем среднюю границу дохода на семью. В этом случае семья может увеличивать свои расходы, и в дальнейшем женщина может оставить работу и посвятить себя домохозяйству.

Условие (5).

Нет возможности выбирать какую-либо из стратегий адаптивного поведения в условиях кризиса. Следовательно, семья не может адаптироваться к кризису, она имеет недостаточный капитал при обоих работающих супругах в семье, расход ниже прожиточного минимума для выживания и это ведет к распаду семьи. Распад семьи показатель неадаптированности семьи.

Проанализируем, при каких условиях происходит смена идентичности женщин. До экономического кризиса, с повышением дохода семьи растет доля женщин, которые предпочитают семью работе, и наоборот. Таким образом, уменьшение занятости женщин в общественном производстве, их ориентация на семейные енности обусловлены тем, что у мужчин имеется возможность хорошо зарабатывать и обеспечивать семью достаточным капиталом . Расход семьи при этом намного выше прожиточного минимума ).

Экономический кризис ломает сложившийся образ жизни, и в семьях, где мужчины имеют достаточный уровень толерантности к профессиональной активности женщин, для того чтобы семьи выжила женщины с высокой творческой энергией и адаптивными способностями идут работать.

2.1.3 Компьютерный эксперимент

Построенная нами модель реализована на языке Objective – C мульти-агентной системе моделирования SWARM. Возможности встроенного графического интерфейса пользователя в данном пакете позволяют визуально наблюдать за ходом развития процесса. С помощью специального инструментария, содержащегося в основных библиотеках, мы выводим на экран анимационную картину. Выводится среда исследования (сеточная область), на которой располагаются семьи, состоящие из агента-мужчины и агента-женщины, а также отображается количество ресурса в каждой ячейке. Клетки, содержащие семьи с различной идентичностью агентов, окрашены в разные цвета. Степень богатства ресурса в источниках среды различается по цветовой гамме: чем больше ресурс, тем ярче цвет. Таким образом, мы можем выявить более богатый источник дохода. Процесс можно наблюдать как в непрерывном, так и в пошаговом режиме. В любой момент времени можно узнавать значение характеристик семьи, идентичность агентов, вызвав вспомогательное графическое окно на каждую семью. Изменяя в данном окне значение параметров, мы имеем возможность переместить семью к другому источнику дохода, поменять ее характеристики.

При первоначальном запуске программы-модели появляется пользовательская панель управления, позволяющая переключать режимы работы (остановка, непрерывный и пошаговый режим, сохранение любого этапа имитации), панель начальный данных модели, где отображаются начальные значения параметров, которые устанавливаются исследователем.

Для описанной выше модели проведены компьютерные эксперименты подобраны значения характеристик, при которых поведения агентов согласуется с моделируемой ситуацией. Рассматривалось поведение семьи до, во время и после экономического кризиса. Первоначально в модели задается докризисная ситуация, характеризующаяся семейно-ориентированным образом жизни членов семьи, предполагающем принятие как мужчинами, так и женщинами традиционных ролей, т.е. мужчина работает, а женщина нет.

Рис.7.1. Стадия жизни в семье в стабильном обществе.

Семьи располагаются случайным образом, имея определенные внутренние характеристики: начальный капитал, уровень адаптации, толерантности, степень идентичности женщины в семье, коэффициенты дохода мужчины, женщины и расхода семьи. Рассматривалось 50 семей (рис.7.1).

Темными точками отображаются семьи с двумя работающими супругами, светлыми – семьи, в которых муж обеспечивает семью полностью. Вокруг агентов с различной яркостью квадратики, характеризирующие наличие ресурса в источниках дохода семьи. Через некоторые промежутки времени происходит то уменьшение ресурса в источниках дохода семьи, то увеличение. Задача агентов состоит в поддержании равновесия между доходом и потреблением ресурсов в семье.

В период ростов доходов большая часть агентов-женщин ориентированы на семью (рис. 7.1).

но приходит время, когда резкое сокращение ресурсов в источниках доходов ведет к наступлению экономического кризиса в семье. В этом случае агентам необходимо сориентироваться и выбрать наиболее приемлемую для их семь стратегию адаптивного поведения. Это может быть:

1. поиск более денежной работы (агенты перемещаются ближе к наиболее богатым местам расположения ресурсов);
2. снижение притязаний ( агенты вынуждены в связи с острой нехваткой доходов сократить свои расходы);
3. смена идентичности – агент-женщина с высокой персональной активностью может изменить на время кризиса семейную ориентацию на профессиональную.

Рис.7.2. Семьи искусственного общества в состоянии экономического кризиса

Можно видеть, что в случае долгого экономического кризиса большинство агентов-женщин имеют профессиональную ориентацию (рис.7.2).

Если стратегия адаптивного экономического поведения выбрана успешно, то в этих семьях устанавливается баланс роста и потребления ресурса.

По истечении некоторого времени можно наблюдать изменение начального капитала, коэффициента расхода семьи, самоидентичности женщин, количество семей преодолевших кризисную ситуацию, а также увеличение/уменьшение ресурса в источниках дохода с определенным периодом. Мы можем устанавливать временные периоды экономических кризисов и стабильного развития. В данном примере период равен 400. Таким образом, сначала мы задаем этап стабильного развития общества, а затем при наступает период экономического кризиса и т.д.

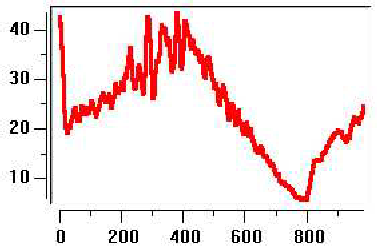
Рис.7.3. Динамика изменения капитала семьи.

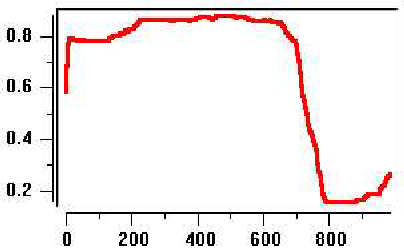
Рис.7.4.график изменения коэффициента расхода капитала семьи

На рис 7.3. дана динамика изменения капитала семьи. На промежутке времени (0.400) наблюдается колебательный рост капитала семьи. В момент времени (заданное время наступления экономического кризиса) происходит резкое уменьшение наличного капитала. Жизнь становится дороже, а доходы все меньше ( количество ресурса с наступлением кризиса в источниках дохода уменьшается).

По окончании экономического кризиса постепенно капитал семьи начинает возрастать.

На рис.7.4. изображен график изменения коэффициента расхода капитала семьи со временем. В период стабильного развития (0.400) коэффициент расхода семьи возрастает в соответствии с ростом наличного капитала семьи (рис.7.3) и со временем стабилизируется. С наступлением экономического кризиса ( малая часть семей уменьшает свои расходы, но большинство придерживаются старого коэффициента расхода, т.е. они пытаются сохранить прежний образ жизни. Но в момент времени (), когда капитал семьи (рис.7.3) падает ниже заданной границы, означающей острый экономический кризис в семье (), основное количество семей вынуждено резко снизить свои расходы. После экономического кризиса некоторое время коэффициент расхода семьи сохраняется малым. Это объясняется тем, что семьи находятся еще в ожидании то, что жизнь станет труднее материально, и боятся, смогут ли они приспособиться, если сразу повысят свои расходы. В дальнейшем, когда капитал семьи превышает среднюю границу дохода, семья начинает понемногу увеличивать расходы. Но не до того уровня, который наблюдался до экономического кризиса. Следовательно, первоначально, во время кризисной ситуации, большинство семей не хотят расставаться с первичным уровнем жизни и, используя внутренние резервы семьи, выбирают такие стратегии адаптивного поведения, как поиск более денежной работы и выжидательная стратегия. Можно заключить, что стратегия. Можно заключить, что стратегия снижения расходов востребывается семьей в ситуации острого экономического кризиса.

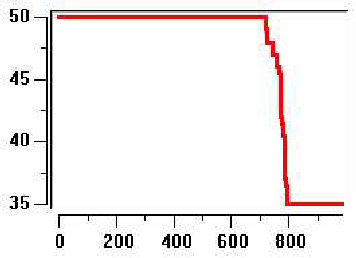
Рис.7.5. график изменения количества семей

На рис.7.5. дан график изменения количества семей со временем. Из графика видно, что количество семей в период кризиса некоторое время сохраняется ( происходит выбор различных стратегий адаптивного поведения), но позже (), когда капитал семьи намного ниже прожиточного минимума инет успешной стратегии выживания, семья находится на «краю» устойчивости, и происходит распад некоторого количества семей. С прекращением экономического кризиса количество семей опять стабилизируется.

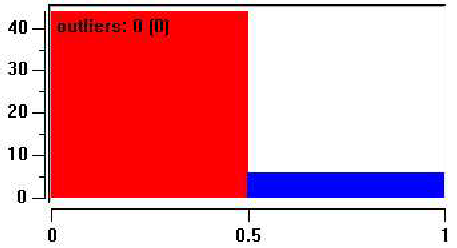
Рис.7.6. диаграмма соотношения количества семей с различной идентичностью женщин.

На рис.7.6. диаграмма отражает изменение соотношения количество семей с профессиональной и семейной идентичностью женщин. Первый стбец показывает количество семей, в которых женщина семейно-ориентирована, второй – профессионально-ориентированна. Проанализируем, когда происходит изменения идентичности женщины в семье. Из диаграммы на рис.7.6 видно, что большинство женщин до кризиса не работают в соответствии с традиционным образом семьи.

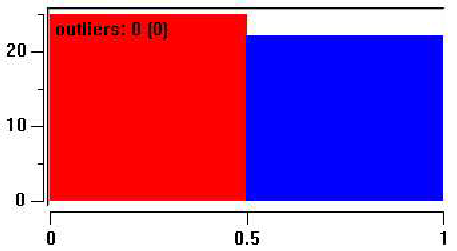
Рис.7.7: диаграмма соотношения при наступлении экономического кризиса

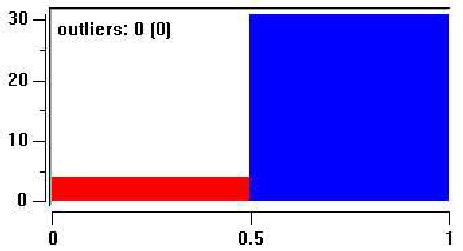
Рис.7.8: диаграмма соотношения в период острого кризиса

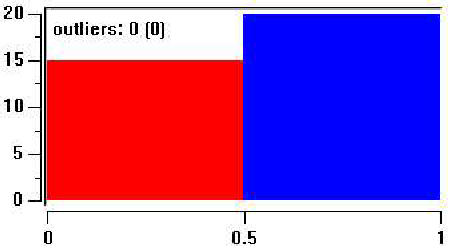
Рис.7.9: диаграмма соотношения при преодолении экономического кризиса

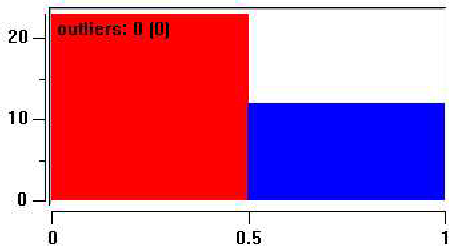
Рис.7.10:диаграмма соотношения на этапе стабильного развития

С наступлением экономического кризиса растет доля профессионально-ориентированных женщин (рис.7.7).

в период острого кризиса подавляющее большинство женщин вынуждены работать. Здесь уже муж и жена делят между собой ответственность за финансовое обеспечение семьи (рис.7.8).

Стратегия «домашней хозяйки» формируется по мере преодоления экономического кризиса и достижения стабильности в обществе (рис.7.9).

В дальнейшем, на этапе стабильного развития общества, явно перевешивается чаша весов в сторону семей, в которых женщины не работают, поскольку доход мужа обеспечивает высокий жизненный уровень (рис.7.10).

Полученные результаты говорят не столько об удельном весе той или иной стратегии, сколько о тенденциях поведения семей в стремлении преодолеть кризисную ситуацию. Выявленное в исследовании различие стратегий показывает, что основным внутренним резервом при наступлении экономического кризиса, который пытается использовать семья, является возможность женщины сменить семейную ориентацию на профессиональную. Это дает дополнительный доход семье и возможность преодолеть экономический кризис.

2.2 Модель “хищник-жертва”

Рассмотрим другую форму сосуществования двух биологических видов, когда первый из них служит пищей для второго. Если бы в данной среде обитал только первый вид (жертва), то он имел бы естественный прирост , который считается постоянным и положительным ( предполагается, что жертвы не испытывают недостатка в пище).Тогда в отсутствии хищников наблюдался бы экспоненциальный рост численности жертв. Если же второй вид хищников существует изолированно, то из-за нехватки пищи(т.е. жертв) он имел бы отрицательный прирост численности — коэффициент вымирания хищников в отсутствии жертв. Исходом здесь было бы полное вымирания хищников.

При сосуществовании видов на ограниченной территории они оказывают серьезное влияния друг на друга. Очевидно, прирост численности жертв должен сократиться, причем тем больше, чем выше число хищников. Это объясняется тем, что большее количество хищников нуждается в соответствующим количество пищи, в качестве которой приходится выступать многострадальным жертвам. С другой стороны, прирост хищников должен возрасти тем сильнее, чем выше численность жертв, поскольку в этих условиях большее число хищников будет обеспеченно полноценной пищей. В результате получаем дифференциальное уравнения

Где коэффициенты и характеризует изменения прироста жертв и хищников за счет их естественного взаимодействия между собой. Уравнения с соответствующими начальными условиями образуют широко известную математическую модель “хищник-жертва”.

Для исследования полученный системы воспользуемся достаточно распространенным приемом, связанным с заменой переменных. Определим величины

Г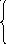де константыa, b и c подбираются таким образом, чтобы получаемые уравнения имели как можно более простой вид. В результате установим соотношения

(6.8)

Где ,.

Определив параметры

П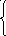олучаем соотношения

(6.9)

называемые уравнениями Вольтерра-Лотки. Системы (6.9) и (6.8) имеют один и тот же смысл. Действительно функции состояния и , а также независимая переменная отличается от величин и t соответственно исключительно постоянными множителями. Таким образом, мы по-прежнему имеем дело с численностями видов и временем, но рассматриваемыми в другом масштабе.

Очевидно, уравнения (6.9) имеют два положения равновесия Первое из низ тривиально, реализуется при отсутствии обоих видов и не представляет никакого практического интереса. Существенно более интересно второе положение равновесия системы. Здесь число вновь родившихся за некоторое время жертв компенсируется их числом, съеденным за то же самое время хищниками. В свою очередь, у хищников рождаемость и смертность также совпадает. Вследствие этого численность обоих видов со временем не меняется, т.е. система находится в состоянии динамического равновесия.

Рассмотрим поведение исследуемой системы вне положения равновесия. Отметим, что численности видов заведомо не отрицательны. Равенство нулю начальной хищников при положительном значении начальной численности жертв приводит к уравнению решение которого экспоненциально возрастет. Таким образом, в отсутствии естественных противников и ограничении на пищу жертвы неограниченно размножаются. Отсутствие жертв в начальный момент времени позволяют получить следующие уравнение относительно численности хищников отсюда следует, что отсутствии пищи хищники постепенно вымирают. Для дальнейших исследований достаточно рассмотреть с положительными начальными состояниями.

Как видно из уравнений (6.9), существует четыре области в фазовой плоскости, различающиеся между собой в смысле поведения рассматриваемой системы(рис.38).

Если в некоторый момент времени t выполняются неравенства

0 Е2/а21 Е1/а12 < Е2/а22 1/2 > 2/5, 1/3 > 2/4

Но, в какой то момент времени, после рождения малыша, Е2(степень влияния жены) резко увеличиться в несколько раз. Тогда их борьба будет выглядеть следующим образом:

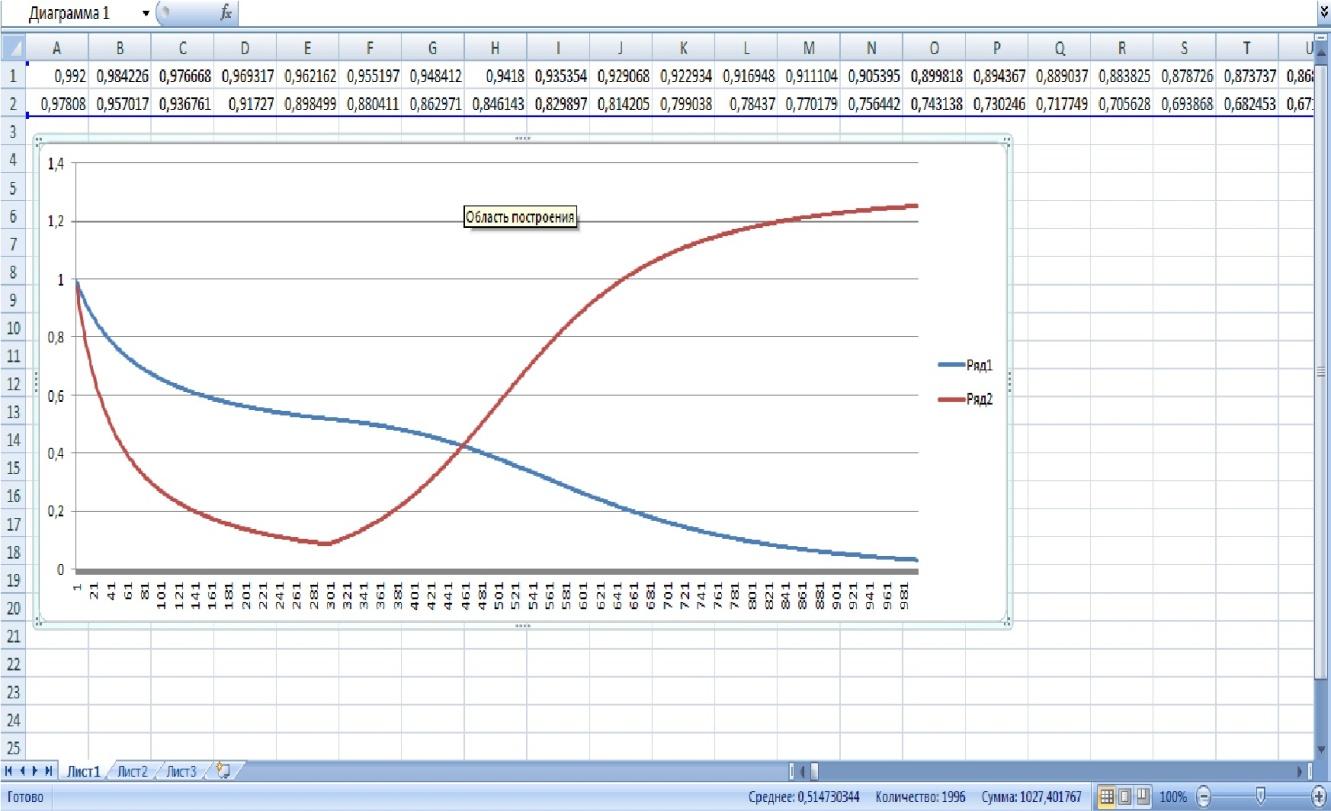
2. В случае внезапной болезни свекрови, то Е1(степень влияния матери) возрастает. И тогда Е1/а11 > Е2/а21 Е1/а12 < Е2/а22 1/2 > 2/5, 1/3 > 2/4

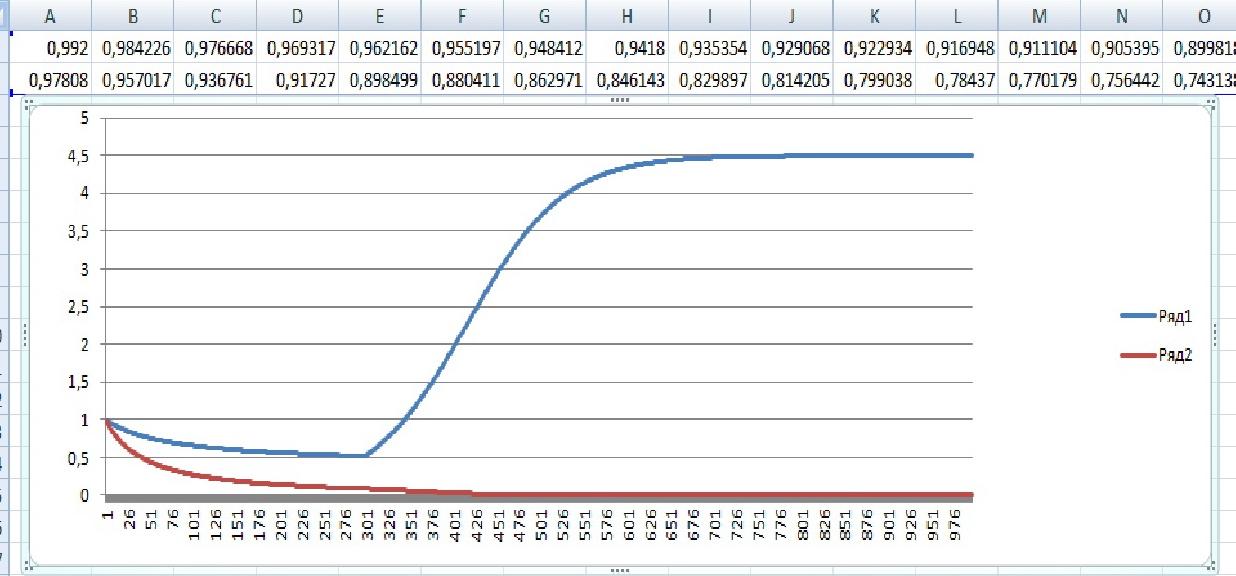
Описанная модель никак не учитывает реакцию на происходящие события самого виновника и предмета разговоров. Однако так ли уж нужно спрашивать мнение авторитетного главы семьи, когда серьезный спор идет между любящими представительницами слабого пола? Впрочем, отношения между тещей и зятем характеризуются не менее захватывающими событиями.

2.4 Исследование математической модели на устойчивость

И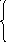сследуем нашу математическую модель на устойчивость по Ляпунову.

Для начала нужно правую часть нашего уравнения приравнять к нулю. Получается корнем нашего уравнения будет:

1. 

2. 

Используя написанный программный код на С++ получаем следующие графики:

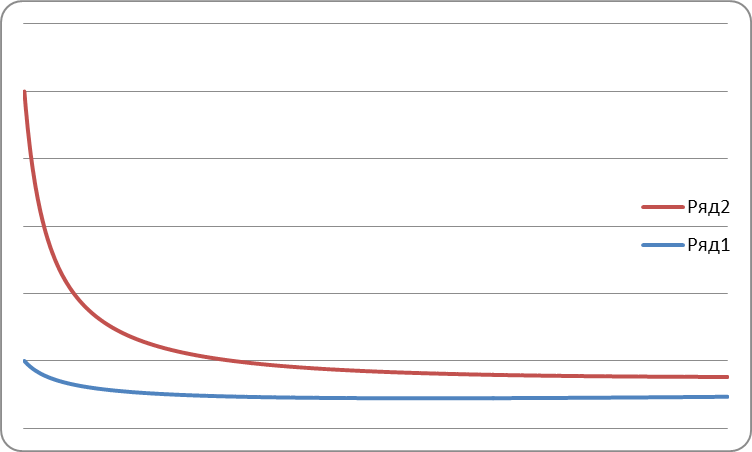
Используя график, мы видим, что при введении любых положительных значении для всех переменных, функции будут стремиться либо к нулю, либо к своему второму корню уравнения, что подтверждает устойчивость функции.

2.5 Модель Профсоюзная деятельность

Рассмотрим простую динамическую модель профсоюзной деятельности на производстве. Функциями состояния здесь будут степень влияния профсоюза и социальные условия на рассматриваемом предприятии. Предполагается, что при существенном ухудшении социальных условии влияние профсоюза растет с некоторой скорость , а при полном отсутствии влияние профсоюза социальные условия ухудшаются с постоянной скоростью . Рост влияния профсоюза сопровождается улучшением социальных условии, что, в свою очередь, приводит к падению влияния профсоюза. Таким образом, математическая модель рассматриваемого процесса принимает вид:

Начальные условия для данного вида уравнений будет:

Где константы r1 и r2 являются параметрами задачи.

Присвоим значение e1=0.5, e2=2 . тогда график для нашего уравнение будет выглядеть следующим образом:

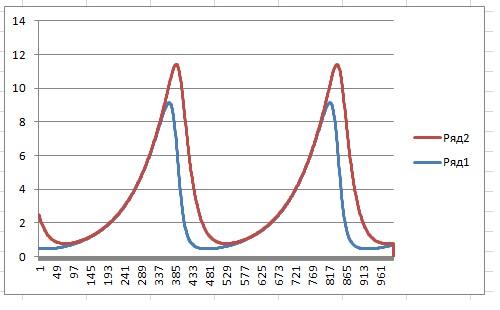
Приведенные уравнения могут встречаться при описании химических, биологических и экономических процессов. Как известно, они имеют периодическое решение (рис.45).

Если в начальный момент времени влияние профсоюза достаточно слабое, а социальные условия — низкие, то правая часть первого уравнения положительна, а второго – отрицательна. Таким образом, на первой стадии процесса наблюдается рост влияния профсоюза (все больше трудящихся при плохих социальных условиях на производстве обращается за помощью к профсоюзу) и дальнейшее ухудшение социальных условий ( при слабом влиянии профсоюза жадный предприниматель старается извлечь максимальную прибыль за счет жестокой эксплуатации бесправных трудящихся).

С ростом влияния профсоюза непременно наступает момент перехода ко второму этапу, когда предприниматель уже вынужден считаться с профсоюзом и под угрозой забастовки идет на определенное удовлетворение справедливых требований своих сотрудников. Происходит улучшение социальных условий при непрекращающемся росте влияния профсоюза ,пользующегося все возрастающей поддержкой рабочих и служащих. Однако по мере подъема жизненного уровня у неблагодарных людей постепенно отпадает необходимость оказывать поддержку профсоюзу. На третьем этапе влияние профсоюза начинает падать, в то время как социальные условия на производстве пока еще растут, поскольку профсоюз остается еще достаточно сильным, а потому предприниматель не рискует проводить какие либо нехорошие мероприятия. Однако с падением влияния профсоюза корыстолюбивый собственник начинает бороться за повышение своих доходов. На четвертом этапе наблюдается дальнейшее снижение влияния профсоюза (социальные условия еще сравнительно высоки, и профсоюз не успел набрать силу)и ухудшение жизненных условий. По мере ухудшения уровня жизни трудящихся со временем профсоюз вновь восстанавливает свое влияние и процесс повторяется.

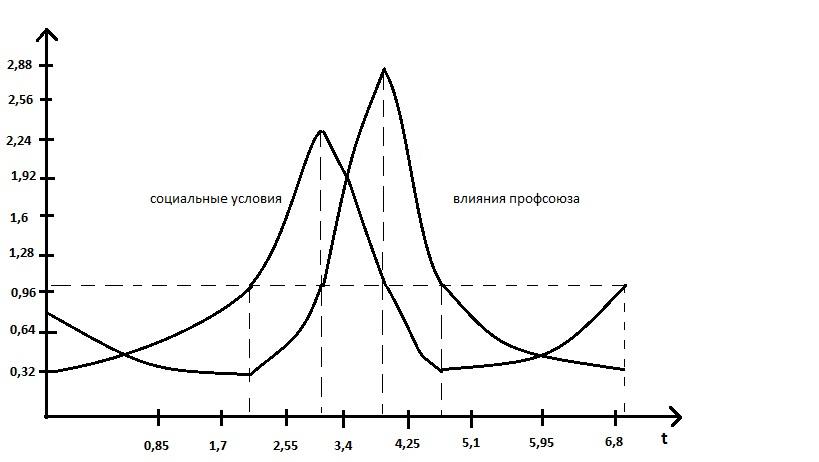
Рис.45 колебание влияния профсоюза и социальных условий на производстве

Заключение

Данный дипломный проект, написан четко опираясь на поставленные цели и задачи. Были рассмотрены актуальные социально-психологические проблемы общества, выявлены наиболее актуальные 2 проблемы. Была построена математическая модель среднестатистической семьи до экономического кризиса, во время экономического кризиса, и после. Также было рассмотрено ряд дополнительных факторов, которые смогли бы влиять на изменение внутреннего капитала семьи.

Опираясь на всеми известную математическую модель «хищник-жертва», была построена математическая модель отношений в семье. Предполагалось, что семья состоит из 3 человек, и с помощью написанного программного кода на языке программирования с++, были выявлены все возможные развития отношении в семье. После написания кода, и выявления всех факторов влияющих на изменение математической модели, были сделаны определенные выводы, при которых отношения в семье будут развиваться в положительную, либо отрицательную сторону. После построения модели адаптивного поведения семьи, был сделан вывод, что стабильность и адаптивное поведение семей в течение экономического кризиса связаны с разнообразными формами индивидуального и совместного действий, например с персональной активности членов семьи и совместимостью гендерных ролей;

Также, основываясь на модели «хищник-жертва», нами была рассмотрена профсоюзная деятельность в одной фирме. А именно, были рассмотрены развитие отношений между профсоюзом, работниками и главой фирмы. С помощью написанного нами программного кода также на языке программирования с++, был построен график, позволяющий прогнозировать зависимость между социальными условиями и влиянием профсоюза.

Все поставленные цели и задачи были выполнены.