Частное образовательное учреждение высшего профессионального образования «восточно-европейский институт психоанализа»

метки: Вероятность, Высокий, Математик, Глава, Событие, Специальность, Ильин, Гуманитарный

Частное образовательное учреждение высшего профессионального образования «восточно-европейский институт психоанализа»

Утверждаю

Первый проректор

К. псх. н.

_______________________

Муханова Н. А.

«______»___________2012 г.

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ

«Математическая статистика» Направление подготовки 030300 — Психология

Квалификация выпускника: бакалавр психологии

Санкт-Петербург, 20___г.

В результате изучения дисциплины студент должен:

Знать:

— понятие отображения, функции и ее графика

Цели и задачи изучения дисциплины. Направление подготовки: Психология

... Требования к содержанию и уровню усвоения учебной дисциплины «Психология семьи" ................ - 3 - 2. Цели и задачи изучения дисциплины............................................. - 4 - 3. Объем дисциплины и виды учебной работы............................... - 5 - 3.1. Объем ...

— основные определения дискретной математики, теории множеств, математической логики, математического анализа, алгебры, теории вероятностей и математической статистики, линейной и векторной алгебры в пределах программы данного курса как базовые понятия, являющиеся основанием математической статистики

— понятие случайной величины, закона ее распределения, функции распределения, ее свойств и графика

— связь между понятием случайной величины, генеральной совокупности и выборки

— понятие статистической гипотезы, статистики и статистического критерия

— основные виды статистического анализа и их теоретическую основу

Уметь:

—решать элементарные задачи , связанных с различными вариантами определения понятия вероятности

— найти закон распределения, функцию распределения и числовые характеристики данной случайной величины

— сформулировать статистическую задачу, связанную с данным экспериментом и представить схему ее решения

— поставить задачу о наличии зависимости между рассматриваемыми величинами и составить схему выявления ее наличия и характера

Владеть:

• основными понятиями математической статистики, представлениями об их основах и связи с теорией вероятностей
• приемами работы со специальной литературой, информационной поисковой работы и приемами критического анализа научной информации
• основными представлениями о методологии и технологии различных видов статистических задач

1. Цели и задачи дисциплины:

Цель:формирование базовых знаний по теории вероятностей и математической статистике, их связи с основными разделами высшей математики, развитие у студентов навыков математического мышления; навыков использования математических методов, в том числе статистических, и, как итог,  математической культуры;

Задачи:

• приобретение знаний об основных понятиях математики (теория множеств, математический анализ, дискретная математика, теория вероятностей) как основе математической статистики
• приобретение навыков самостоятельной работы, работы с литературой (разбор ряда теоретических вопросов, решение задач, работа с результатами исследований)
• формирование представления о теории вероятностей и математической статистике как инструменте психологических исследований; формирование основной понятийной базы для последующего изучения курса «Математические методы в психологии»
• формирование представлений о математической основе практических методов, используемых для обработки результатов в психологических исследованиях

Дисциплина «Математическая статистика» относится к математическому и естественно-научному циклу (базовая часть).

Учебный курс «Математическая статистика» знания студентами курса математики средней школы и является базой для последующего изучения курса «Математические методы в психологии», а также курсов «Экспериментальная психология и «Психодиагностика». Поэтому изучение предмета целесообразно на I-II курсах.

Требования к результатам освоения дисциплины:

Процесс изучения дисциплины направлен на формирование следующих компетенций: ОК-2, ОК-3, ОК-4, ОК-5, ОК-9, ОК-10, ОК-11, ОК-12, ПК-2

4. Объем дисциплины и виды учебной работы

Вид учебной работы	Всего часов	Семестры
		III
Аудиторные занятия (всего)	69
В том числе:	—	—	—	—	—
Лекции		50
Практические занятия (ПЗ)		13
Контроль самостоятельной работы студентов (КСР)		4
Консультация перед экзаменом		1
Предварительная аттестация		1
Самостоятельная работа (всего)	76
В том числе:	—	—	—	—	—
Работа с текстом лекций и литературой, самостоятельный разбор отдельных вопросов курса		36
Решение текущих домашних работ		36
Решение домашних контрольных работ		4
Вид промежуточной аттестации (зачет, экзамен)	экзамен
Общая трудоемкость часы зачетные единицы	144

5. Содержание дисциплины

5.1. Содержание разделов дисциплины

№ п/п	Наименование раздела дисциплины	Содержание раздела
1.	Основы теории вероятностей	Глава 1.1.Случайные события и их вероятности Раздел 1.1.1. События Случайные события. Совместные и несовместные события. Элементарные события. Противоположные события. Равновозможные события. Пространство элементарных событий Раздел 1.1.2. Определения вероятности Вероятностное пространство Случай конечного или счетного числа исходов. Классическое определение вероятности Статистическое определение вероятности Геометрические вероятности РазРаздел 1.1.3.Вероятностная модель эксперимента с бесконечным числом исходов. Аксиоматика Колмогорова σ-алгебра событий. Вероятностное пространство. Аксиоматическое построение теории вероятностей Раздел 1.1.4 Условные вероятности. Независимость событий Независимые события. Теоремы о сложении и умножении вероятностей Формула полной вероятности Формула Байеса Глава.1.2.Последовательность независимых испытаний Повторные независимые испытания. Схема Бернулли. Формула Бернулли Предельные теоремы для схемы Бернулли: Локальная теорема Муавра-Лапласа. Функция Гаусса Интегральная теорема Муавра-Лапласа. Функция Лапласа Теорема Пуассона Глава 1.3.Случайные величины и функции распределения Раздел 1.3.1.Понятие случайной величины. Понятие случайной величины Функция распределения случайной величины, ее свойства Раздел 1.3.2. Случайные величины с дискретным распределением Понятие случайной величины с дискретным распределением Закон распределения дискретной случайной величины. Примеры дискретных распределений Раздел 1.3.3.Случайные величины с абсолютно непрерывным распределением Понятие случайной величины с абсолютно непрерывным распределением Закон распределения абсолютно непрерывной случайной величины. Плотность, ее свойства Примеры абсолютно непрерывных распределений Раздел 1.3.4.Понятие случайного вектора. Понятие случайного вектора Независимые случайные величины Совместное распределение случайных величин Раздел 1.3.5.Функции от случайных величин Глава 1.4.Числовые характеристики случайных величин Понятие параметров распределения Математическое ожидание и его свойства Дисперсия и ее свойства Ковариация и коэффициент корреляции Моменты Неравенства Маркова и Чебышева Квантиль, асимметрия, эксцесс, мода, медиана Глава 1.5. Последовательность случайных величин Виды сходимости последовательности случайных величин. Закон больших чисел Центральная предельная теорема

2.

Введение в математическую статистику

Введение 2 Глава 2.1. Закон распределения генеральной совокупности и первичное представление данных Понятие случайной выборки, генеральной совокупности, функции правдоподобия. Вариационный ряд. Эмпирическая функция распределения. Выборочное среднее и выборочная дисперсия Глава 2.2. Статистические оценки Понятие оценки как функции выборки. Виды оценок Точечные оценки. Свойства несмещенности, состоятельности и эффективности. Отыскание оценок методом моментов. Метод максимального правдоподобия. Интервальные оценки. Доверительные интервалы и области. Глава 2.3. Статистическая проверка гипотез. Основные задачи статистики в терминах функции распределения Понятие статистической гипотезы. Общее понятие о статистической проверке гипотез. Простые и сложные гипотезы. Понятие статистики как функции выборки Критерий и его статистика Критическая область. Ошибки первого и второго рода. Параметрические и непараметрические критерии. Примеры Глава 2.4.Элементы корреляционного анализа Понятие функциональной и статистической зависимости Линейная зависимость Причины неправильной интерпретации результатов Отступление. Матрицы Корреляционная матрица Корреляционная плеяда Глава 2.5.Элементы регрессионного анализа Постановка задачи Примеры

5.2. Разделы дисциплин и виды занятий

№ п/п	Наименование раздела дисциплины	Лекц.	Практ. зан.,	Лаб. зан.	Семин	СРС	Всего
1.	Элементы теории вероятностей
2.	Введение в математическую статистику

8.Методические рекомендации преподавателю

Работа по подготовке преподавателя к проведению занятия начинается с анализа учебной программы дисциплины.

При анализе программы следует обращать внимание на следующие моменты:

Особенности и содержание курса и разделов.

Программа курса призвана дать студентам представление об основных понятиях математической статистики , их связи с базовыми понятиями высшей математики, в первую очередь теории вероятностей

2. Связь между отдельными темами.

Ключевым и сквозным понятием курса является понятие вероятности, случайной величины и функции распределения.

В этих терминах формируются задачи и описываются группы методов математической статистики .

3. Логика структурирования материала в программе. Основной задачей курса является представление о постановке статистической задачи, происхождении и основаниях использования конкретных методов. Поэтому большое внимание в курсе уделяется не конкретным методам обработки психологических исследований, а их математическим основам, в первую очередь теории вероятностей. В материале лекций имеются разделы «Отступление» и «Дополнение». «Отступление» содержит минимальную необходимую справочную информацию из курса высшей математики; «Дополнение» — представляющее интерес дополнение к основному материалу, представляющий познавательный и общенаучный интерес и не является обязательным.

Технология преподавания отдельных тем. Преподавание ведется в форме лекций и семинарских занятий, а также самостоятельной работы студентов. Рассмотрение тем раздела «Основы теории вероятностей» основывается на простых. Понятных студентам «бытовых» примерах и примерах из области психологии. При рассмотрении задач статистики рассматриваются математические основы таких разделов как: представление данных, оценивание, проверка статистических гипотез, основы корреляционного и регрессионного анализа

9. Методические рекомендации студенту по организации самостоятельной работы

Изучение курса требует систематической самостоятельной работы студента, поэтому с первых занятий рекомендуется :

— работа с конспектами лекций

— выполнение теоретических заданий, данных в ходе лекций для закрепления полученных знаний, проверки правильности понимания основных понятий, а также формирования умения проводить рассуждения и доказательства

— самостоятельное изучение вопросов курса по учебникам

— конспектирование учебной литературы

— систематическое выполнение домашних работ

— участие в консультационных занятиях и своевременный разбор тем и понятий, оставшихся непонятыми

К самостоятельным видам работы студентов относятся:

— работа с текстом лекций, разбор отдельных вопросов курса, ответ на вопросы для самоконтроля

— решение текущих домашних заданий (образцы заданий с их разбором содержатся в «примерах» в тексте курса, в качестве основных источников задач используются А.А.Гусак, Е.А.Бричникова «Теория вероятностей. Справочное пособие к решению задач» и В.Е.Гмурман «Руководство к решению задач по теории вероятностей и математической статистике»)

— решение двух домашних контрольных работ. Примерный вид работ:

Раздел «Введение в теорию вероятностей»

7. Х – случайная величина, равная сумме очков на верхних гранях

двух одновременно брошенных кубиков. Построить закон

распределения, функцию распределения с графиком, найти мат.

ожидание, дисперсию, моменты до 3 порядка

8. Дана плотность распределения случайной величины ρ(х) =

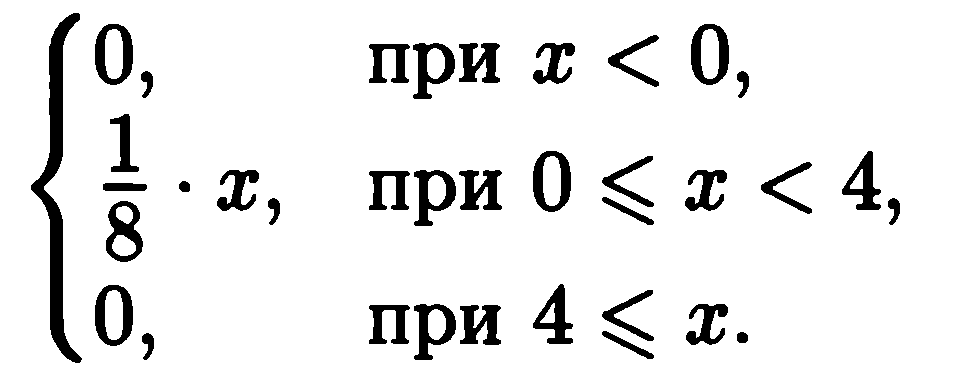
Построить закон распределения, функцию распределения с графиком, найти мат.ожидание, дисперсию, моменты до 3 порядка

9. Построить график плотности и функции распределения, найти параметры табличного распределения

10. Дана плотность распределения ρ(х) =

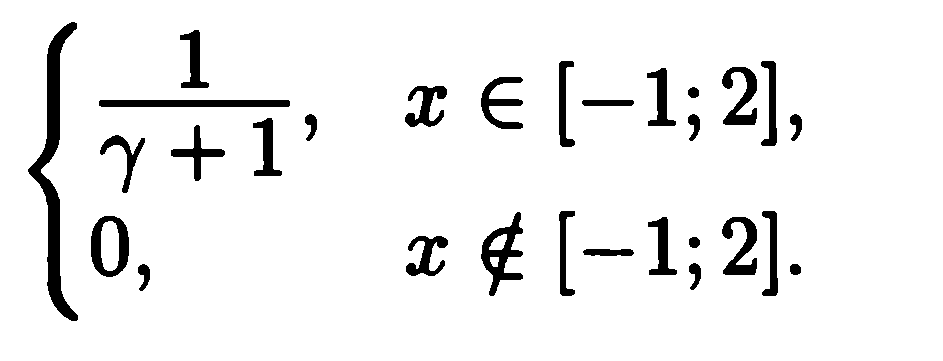
Найти значение γ, найти ЕХ и DX

11.

.

Построить законы распределения Х и Y, найти ковариацию и коэффициент корреляции X и Y

12.

.

13.

14. Используя центральную предельную теорему, решить:

Раздел «Введение в математическую статистику»

1.

Дана выборка объема n=100 . Результаты измерений и частоты представлены в таблице

0,2 1,4 2,6 3,8 5 6,2 7,4

5 13 25 25 19 10 3

Построить выборочный закон распределения, выборочную функцию распределения с графиком,

Построить полигон частот. Найти выборочные мат.ожидание, дисперсию

2. Найти доверительный интервал для оценки неизвестного математического ожидания a нормального распределения с α=0,95 . Известно выборочное среднее = 10,43 , объем выборки = 100 и среднеквадратичное отклонение, равное 5

3. В городе 17036 семей имеют двоих детей, в

Определить задачу статистики, соответствующую группу критериев, представить схему решения.

4. Каждый из 6800 человек исследовался по

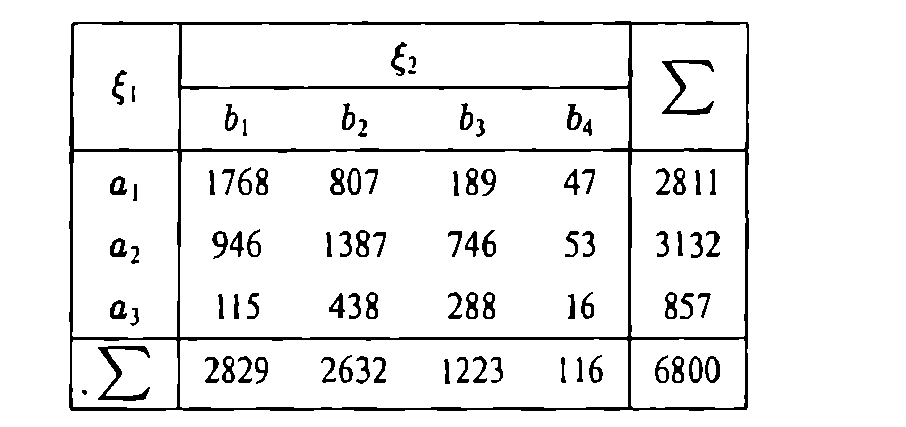
Представить схему ответа на вопрос о независимости цвета глаз и цвета волос при α =0,05

5. В книге «Основы химии» Д.И.Менделеева

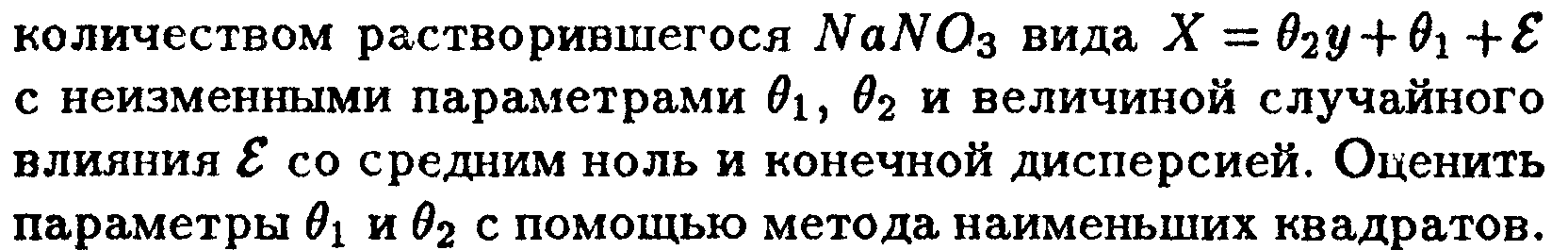
10. Вопросы к предварительной аттестации

1. Случайные события. Совместные и несовместные события. Элементарные события. Противоположные события. Равновозможные события. Пространство элементарных событий
2. Классическое определение вероятности
3. Статистическое определение вероятности
4. Геометрические вероятности
5. Статистическая оценка неизвестных вероятностей
6. Условные вероятности
7. Независимые события. Теоремы о сложении и умножении вероятностей
8. Формула полной вероятности
9. Формула Байеса

10. Схема Бернулли. Предельные теоремы для схемы Бернулли
11. Локальная теорема Муавра-Лапласа
12. Интегральная теорема Муавра-Лапласа
13. Теорема Пуассона

14. σ-алгебра событий. Вероятностное пространство.
15. Аксиоматическое построение теории вероятностей
16. Понятие случайной величины.
17. Закон распределения случайной величины. Случайные величины с дискретным и абсолютно непрерывным распределением
18. Функция распределения случайной величины, ее свойства. Параметры распределений
19. Примеры дискретных распределений
20. Плотность, ее свойства
21. Примеры абсолютно непрерывных распределений
22. Математическое ожидание, дисперсия, центральный и начальный моменты случайной величины
23. Понятие случайной величины. Закон распределения случайной величины.
24. Случайные величины с дискретным и абсолютно непрерывным распределением
25. Функция распределения случайной величины, ее свойства. Параметры распределений
26. Примеры дискретных распределений
27. Плотность, ее свойства
28. Примеры абсолютно непрерывных распределений

11.Вопросы для подготовки к экзамену. Раздел 1. Основы теории вероятностей

29. Случайные события. Совместные и несовместные события. Элементарные события. Противоположные события. Равновозможные события. Пространство элементарных событий
30. Классическое определение вероятности
31. Статистическое определение вероятности
32. Геометрические вероятности
33. Статистическая оценка неизвестных вероятностей
34. Условные вероятности
35. Независимые события. Теоремы о сложении и умножении вероятностей
36. Формула полной вероятности
37. Формула Байеса

38. Схема Бернулли. Предельные теоремы для схемы Бернулли
39. Локальная теорема Муавра-Лапласа
40. Интегральная теорема Муавра-Лапласа
41. Теорема Пуассона

Функции от случайных величин

42. σ-алгебра событий. Вероятностное пространство.
43. Аксиоматическое построение теории вероятностей
44. Понятие случайной величины.
45. Закон распределения случайной величины. Случайные величины с дискретным и абсолютно непрерывным распределением
46. Функция распределения случайной величины, ее свойства. Параметры распределений
47. Примеры дискретных распределений
48. Плотность, ее свойства
49. Примеры абсолютно непрерывных распределений
50. Математическое ожидание, дисперсия, центральный и начальный моменты случайной величины
51. Понятие случайной величины. Закон распределения случайной величины.
52. Случайные величины с дискретным и абсолютно непрерывным распределением
53. Функция распределения случайной величины, ее свойства. Параметры распределений
54. Примеры дискретных распределений
55. Плотность, ее свойства
56. Примеры абсолютно непрерывных распределений
57. Понятие случайного вектора. Независимые случайные величины
58. Математическое ожидание и его свойства
59. Дисперсия и ее свойства
60. Ковариация и коэффициент корреляции
61. Моменты
62. Неравенство Чебышева
63. Виды сходимости последовательности случайных величин. Закон больших чисел
64. Центральная предельная теорема

Раздел 2. Математическая статистика

1. Задачи математической статистики. Понятие случайной выборки, генеральной совокупности, функции правдоподобия. Представление данных. Вариационный ряд. Гистограмма. Эмпирическая функция распределения. Выборочное среднее и выборочная дисперсия
2. Понятие оценки. Виды оценок
3. Точечные оценки. Свойства несмещенности, состоятельности и эффективности. Отыскание оценок методом моментов. Метод максимального правдоподобия.
4. Интервальные оценки. Доверительные интервалы и области.
5. Статистическая проверка гипотез. Общее понятие о статистической проверке гипотез. Простые и сложные гипотезы. Критерий, статистика критерия и критическая область. Ошибки первого и второго рода.
6. Принципы использования параметрических и непараметрических критериев.
7. Задача и критерии однородности
8. Задача и критерии согласия
9. Задача и критерии независимости
10. Принципы корреляционного анализа
11. Принципы регрессионного анализа

Экзамен проводится в форме тестирования

12. Примеры задания для итогового тестирования

1. Указать пространство элементарных событий, связанной с данным экспериментом
2. Найти вероятность (классическую, статистическую, геометрическую) данного события
3. Решить задачу с использованием формулы Байеса
4. Решить задачу с использованием формулы полной вероятности
5. Решить задачу с использованием формулы Бернулли
6. Решить задачу с использованием одной из 3х предельных теорем в схеме Бернулли (Локальная теорема Муавра-Лапласа, теорема Пуассона, Интегральная теорема Муавра-Лапласа)
7. Построить закон распределения данной случайной величины
8. Найти функцию распределения данной случайной величины и построить ее график
9. Найти плотность распределения случайной величины по функции распределения и функции распределения по плотности
10. Решить задачу с использованием известных (табличных) законов распределения
11. Найти математическое ожидание, дисперсию, моменты (начальный и центральный) данного порядка данной случайной величины

29. Построить закон распределения данной случайной величины
30. Найти функцию распределения данной случайной величины и построить ее график
31. Найти плотность распределения случайной величины по функции распределения и функции распределения по плотности
32. Решить задачу с использованием известных (табличных) законов распределения
33. Найти математическое ожидание, дисперсию, моменты (начальный и центральный) данного порядка, коэффициент корреляции данных случайных величин
34. Ответить на вопрос о независимости случайных величин по их совместному закону распределения
35. Решить задачу с использованием неравенств Маркова и Чебышёва
36. Указать выборочный закон распределения, выборочную функцию распределения, построить график выборочной функции распределения, гистограмму по данным выборочным данным
37. Найти точечные оценки мат. ожидания, дисперсии и моментов
38. Найти интервальные оценки мат.ожидания и дисперсии
39. Указать, к какой из задачи статистики относится данная статистическая задача, сформулировать основную и альтернативную гипотезы
40. Привести схему выбора и использования критерия для решения данной статистической задачи
41. Привести схему использования методов корреляционно анализа для решения данной статистической задачи
42. Привести схему использования методов регрессионного анализа для решения данной статистической задачи
43. Привести схему использования методов регрессионного анализа для решения данной статистической задачи

12. Учебно-методическое и информационное обеспечение дисциплины:

Рекомендуемая литература по курсу «Статистика»

Основная

1. В.А.Ильин, А.В.Куркина «Высшая математика»

Издательство Московского университета 2008.

(Рекомендовано Министерством образования РФ в качестве учебника для студентов высших учебных заведений, обучающихся по специальностям: … , 521000«Психология»,…)

2. К.Л.Чжун, Ф.АитСахлиа «Элементарный курс теории вероятностей»

М., Бином, 2007

Для студентов, преподавателей, исследователей и практиков в…,психологии,…

3. О.Ю.Ермолаев «Математическая статистика для психологов»

Московский психолого-социальный институт, Издательство Флинта 2003 г.

Рекомендовано редакционно-издательским советом Российской академии образования к использованию в качестве учебно-методического пособия

4. А.Н.Бородин «Элементарный курс теории вероятностей и математической статистики» Изд. Лань, 2011

Рекомендовано Министерством образования РФ в качестве учебного пособия для студентов высших учебных заведений, обучающихся по нематематическим специальностям

Дополнительная

1. А.В.Печинкин, О.И.Тескин и др. «Теория вероятностей» МГТУ им. Баумана, 2004
2. В.Феллер Введение в теорию вероятностей и ее применение т.1, 2(М.Мир, 1984)
3. Б.В.Гнеденко Курс теории вероятностей (Наука.Физматлит, 1988)
4. Е.С.Вентцель Теория вероятностей (М: Высшая школа, 1998 г.)
5. Б.В.Гнеденко, А.Я.Хинчин Элементарное введение в теорию вероятностей (М., Наука, 1970)
6. А.Н.Колмогоров Основные понятия теории вероятностей (М.Наука, 1974)
7. М.Б.Лагутин «Наглядная математическая статистика» Бином, 2009
8. В.Б.Горяинов, И.В.Павлов и др. «Математическая статистика» МГТУ им.Баумана, 2006
9. Г.Секкей Парадоксы теории вероятностей и математической статистики (М., Мир, 1990).
10. Г.И.Ивченко и М.И.Медведев «Введение в математическую статистику» URSS, изд-во ЛКИЮ 2010
11. Б.А.Севастьянов «Курс теории вероятностей и математической статистики» М., Наука, 1984
12. Е.Сидоренко Методы статистической обработки в психологии (Речь, 2003)
13. А.Д.Резник «Книга для тех, кто не любит статистику, но вынужден ею пользоваться» Речь, 2008
14. Наследов А. Д. Математические методы психологического исследования: Анализ и интерпретация данных. — СПб., 2007.
15. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004.

При изучении курса было бы полезно иметь под рукой издание по высшей математике, к которому можно было бы обращаться при возникновении вопросов общего характера.

Мы можем порекомендовать в качестве таковых, например,

1. А.В.Дорофеева «Высшая математика. Гуманитарные специальности».

Издательство Московского университета 2004

Рекомендовано Министерством образования РФ в качестве учебного пособия для студентов высших учебных заведений, обучающихся по гуманитарно-социальным специальностям. Для студентов философских факультетов, а также студентов и аспирантов, специализирующихся в области…, психологии,…

2. Я.Стюарт Концепции современной математики (Минск, Вышейшая школа, 1980)

3. Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики»

Москва Астрель АСТ 2004

Учебное пособие для ВУЗов. Пособие предназначено для студентов естественных факультетов университетов

4. Р.Курант, Г.Роббинс «Что такое математика?(Элементарный очерк идей и методов) » МЦНМО, 2001

Книга предназначена для школьников, студентов, преподавателей, а также для всех интересующихся развитием математики и ее структурой

Для ознакомления с математической проблематикой можно было бы рекомендовать, например,

1. В.И.Арнольд «Что такое математика?» МЦНМО, 2011
2. Я.Стюарт Концепции современной математики (Минск, Вышейшая школа, 1980)
3. М.Клейн «Математика: Поиск истины» М, Мир, 1988
4. Г.Вейль «Симметрия» М.Наука, 1968
5. Р.Фейнман, Р.Лейдон, М.Сэндс Фейнмановские лекции по физике т.1 (М.Мир, 1965)
6. Г.Бирхгоф Математика и психология (М., Соврадио, 1977)
7. Е.Б.Дынкин, В.А.Успенский Математические беседы (Физматлит, 2004)
8. И.М.Яглом Необыкновенная алгебра (М.Наука, 1968)
9. П.В.Грес Математика для гуманитариев. Учебное пособие. (М., Логос, 2005)
10. И.Лакатос Доказательства и опровержения. Как доказываются теоремы (ИКЛ, 2010)
11. А.А.Болибрух Проблемы Гилберта 100 лет спустя (М., Изд. МЦНММО, 1999)
12. Дж.Пойа Математическое открытие (М.,Наука, 1967)
13. Дж.Пойа Математика и правдоподобные рассуждения (М., Наука, 1975)
14. Я.Б.Зельдович, М.Ю.Хлопов Драма идей в познании природы Библиотечка «Квант», (М.Наука, 1988)
15. Б.Грин «Элегантная вселенная» URSS, 2010
16. «Трудная задача» Сборник научно-фантастических рассказов на математическую тему М., Мир

Сборники задач

1. К.Н.Лунгу, В.П.Норин и др. Сборник задач по высшей математике , т. 2
2. Л.Д.Мешалкин Сборник задач по теории вероятностей
3. А.А.Гусак, Е.А.Бричникова Теория вероятностей. Справочное пособие к решению задач
4. В.Е.Гмурман «Руководство к решению задач по теории вероятностей и математической статистике»

Ниже приводятся примерные вопросы курса высшей математики с указанием учебных пособий и разделов, к которым можно обращаться в случае необходимости в справочном материале

1.1. Введение

П.1 Место и роль математики в современном мире, мировой культуре и истории, в том числе в гуманитарных науках. Психология и математика. Возможности применения математики в психологии

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Предисловие

А.В.Дорофеева «Высшая математика. Гуманитарные специальности». Глава 15

Г.Бирхгоф «Математика и психология»

Ф.Клейн Элементарная математика с точки зрения высшей т.1 Арифметика Алгебра. Анализ. Часть «Арифметика», глава V, п. 1, 2

Р.Курант, Г.Роббинс Что такое математика? Введение: Что такое математика?

Я.Б.Зельдович «Драма идей в познании природы»

Б.В.Гнеденко «Курс теории вероятностей» Дополнение

П.В.Грес Математика для гуманитариев

П.2 Элементы математической логики

Высказывания и утверждения.

Операции над высказываниями.

Построение отрицаний

Высказывание, зависящее от параметра

Предикаты. Кванторы.

Понятие аксиомы, теоремы, леммы.

Системы аксиом. Евклидова и неевклидовы геометрии

Утверждения и доказательства.

Необходимое и достаточное условие.

Прямая и обратная теоремы

А.Н.Колмогоров, А.Г.Драгалин Введение в математическую логику гл.1, 3

А.Черч Введение в математическую логику, Введение

И.М.Яглом Необыкновенная алгебра § 1, 4, 5

И.Лакатос Доказательства и опровержения. Как доказываются теоремы

Дж.Пойа Математическое открытие гл.3

С.В.Яблонский Введение в дискретную математику Часть I, глава 1

Р.Курант, Г.Роббинс Что такое математика, Глава IV

Я.М.Ерусалимский Дискретная математика Глава 1, 2

А.Соловьев Дискретная математика без формул Лекции 6, 7, 8, 9, 10

П. 3 Числовые множества

3.1. Действительные числа.

Определение множества действительных чисел

Числовые множества

Расширенная числовая прямая.

Модуль вещественного числа.

Свойства модуля

Функция y = |x|

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 1

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 4

Ф.Клейн Элементарная математика с точки зрения высшей т.1 Арифметика Алгебра. Анализ Раздел «Арифметика» Гл. 1 (п. 1-4), 2 (п.1-3), 3 (п.1-7)

А.Я.Хинчин 8 лекций по математическому анализу. Лекция 1

Р.Курант, Г.Роббинс Что такое математика? Глава II, § 1-4, 6

Т.Йех Теория множеств Глава 4

Э.Ландау Курс анализа Глава 2

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т 1, Введение, § 1, 2, 3

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 1

Ф.Клейн Элементарная математика с точки зрения высшей Т.1, Глава «Арифметика»

3.2. Комплексные числа.

Комплексная плоскость

Модуль и аргумент комплексного числа.

Тригонометрическая форма комплексного числа

Арифметические операции над комплексными числами

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 4, п.4.5

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XVI

И.М.Яглом Комплексные числа и их применение в геометрии . Глава 1§ 1, глава 2 § 7,8

Ф.Клейн Элементарная математика с точки зрения высшей т.1 Арифметика Алгебра. Анализ. Раздел «Арифметика» Глава IV, п 1

Я.Б.Зельдович, И.М.Яглом Высшая математика для начинающих физиков и техников Часть 3, глава 14 § 1-4

Э.Ландау Курс анализа Гл.5

Д.К.Фаддеев «Лекции по алгебре» Глава II, пп.1-2

Понятие корня n-й степени из комплексного числа.

Корни из единицы

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XVI , п.14

Д.К.Фаддеев «Лекции по алгебре» Глава II, пп. 3-4

Р.Курант, Г.Роббинс Что такое математика? Глава II, § 5, п. 1-4

Е.Титчмарш Теория функций

1 2. Элементы теории множеств

Понятие множества.

Способы задания. Виды множеств. Примеры

Операции над множествами. Формула двойственности

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 1

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Гл 1 § 1

А.Н.Колмогоров, А.Г.Драгалин Введение в математическую логику гл.1

Н.Я.Виленкин Рассказы о множествах

А.Соловьев Дискретная математика без формул Лекции 1,3

Л.Чжун, Ф.АитСахлиа «Элементарный курс теории вероятностей» Глава 1

Системы множеств

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Гл 1 § 5, п. 1-5

1. 3. Элементы дискретной математики. Отношения и графы

Декартово произведение множеств.

Бинарные отношения. Свойства бинарных отношений. n-арные отношения Отношения эквивалентности и порядка. Связь разбиения множества на классы с эквивалентностью

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 1, пп.1.7 – 1.10

В.Феллер Введение в теорию вероятностей и ее применение т.1, глава II, пп.1-5

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Гл 1 § 2, п.2

Я.М.Ерусалимский Дискретная математика Глава 4

Графы. Определение, свойства, характеристики графов

Основные понятия теории графов.

Ф.Харари Теория графов

С.В.Яблонский Введение в дискретную математику ЧастьIII, глава 1

Я.М.Ерусалимский Дискретная математика Глава 7

1. 4. Элементы комбинаторики

Правило суммы. Правило произведения.

Понятие размещения .Число размещений

Понятие перестановки. Число перестановок

Понятие сочетания. Число сочетаний

В.А.Ильин, А.В.Куркина «Высшая математика»

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть III, глава 4

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 13, п.13.6

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XXV Б, п.10

Н.Я.Виленкин «Популярная комбинаторика» Гл. 1, 2, 3

Н.Я.Виленкин «Комбинаторика» Гл. 1, 2

В.Феллер Введение в теорию вероятностей и ее применение т.1, глава II

Л.Чжун, Ф.АитСахлиа «Элементарный курс теории вероятностей» Глава 3

Я.М.Ерусалимский Дискретная математика Глава 3

Аксиома индукции и следствие из нее. Метод математической индукции

Бином Ньютона. Треугольник Паскаля

Дж.Пойа Математика и правдоподобные рассуждения Гл. 1, 4, 5

Дж.Пойа Математическое открытие Гл.3

Р.Курант, Г.Роббинс Что такое математика? Глава I, § 2, п. 1,5-6

1.5. Введение в математический анализ. Элементы функционального анализа

5.1.Понятие отображения.

Примеры (частные случаи) отображений

Сложное отображение. Сужение отображения

Образ и прообраз множества при отображении. Сюръективное и инъективное отображения. Биекция

Критерий обратимости отображений

Основные свойства отображений

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Гл 1 § 2 п.1

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 10

А.Соловьев Дискретная математика без формул Лекции 4,5

5.2.Числовые множества.

Ограниченные и неограниченные множества. Конечные и бесконечные множества Принцип Архимеда. Усиленный принцип Архимеда

Мощность множества. Счетные и несчетные множества. Счетность рациональных чисел. Несчетность действительных чисел

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 1

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 14

Л.Д.Кудрявцев Краткий курс математического анализа Глава 1, п.4

Ф.Клейн Элементарная математика с точки зрения высшей т.1 Арифметика Алгебра. Анализ. Часть «Приложения», глава II , п. 1-2.

А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа

Гл 1, § 3, п.1-6

А.А.Болибрух Проблемы Гилберта 100 лет спустя. Глава «Первая проблема Гилберта»

5.3.Функции

Понятие функции. График функции.

Способы задания функции

Элементарные функции и их графики.

Линейные, степенные, показательные, и тригонометрические функции

Понятие обратной функции.

Построение графика обратной функции

Преобразование графика.

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 8, п.1

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 5

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава VI

Я.Б.Зельдович, И.М.Яглом Высшая математика для начинающих физиков и техников. Часть 1, глава 1, § 1-9

Л.Д.Кудрявцев Краткий курс математического анализа Глава 1, п.3

Ф.Клейн Элементарная математика с точки зрения высшей т.1 Арифметика Алгебра. Анализ. Часть «Анализ», глава I (п.1-4), II (п.1-3), III (п.1)

Р.Курант, Г.Роббинс Что такое математика? Глава VI, § 1

А.Я.Хинчин 8 лекций по математическому анализу. Лекция III

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 2 , § 43-51

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 2

Ф.Клейн Элементарная математика с точки зрения высшей Т.1, Глава «Анализ»

Понятие функции комплексного переменного

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава ХVI, п.5

Д.К.Фаддеев «Лекции по алгебре» Глава II, п.5

5.4.Теория пределов

Окрестности, их свойства. Точки сгущения и изолированные точки

Определение предела функции. Варианты определения

Понятие числовой последовательности. Предел последовательности.

Определение предела функции на языке последовательностей

Бесконечно малые. Их свойства

Бесконечно большие, их свойства.

Связь между бесконечно большой и бесконечно малой.

Раскрытие неопределенностей

Числа π и e

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 8, пп. 2-5

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 6

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава VII

А.Я.Хинчин 8 лекций по математическому анализу. Лекция II

Л.Д.Кудрявцев Краткий курс математического анализа Глава 1, п.6

В.И.Смирнов Курс высшей математики т.1, Глава I, п.2, пп.25-33

Р.Курант, Г.Роббинс Что такое математика? Глава VI, § 2, п. 1-5 (числа π и e пп. 2, 3), § 3

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 2, § 2, пп. 52, 54, 55, 56

Б.Гилбаум, Дж.Олмстед «Контрпримеры в анализе» Глава 2

Ф.Клейн Элементарная математика с точки зрения высшей Т.1, Приложения, п.1

5.5.Непрерывность функции.

Непрерывность в точке и на промежутке. Классификация точек разрыва

Непрерывность основных элементарных функций

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 9

А.В.Дорофеева «Высшая математика. Гуманитарные специальности»Глава 7

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава VIII

Р.Курант, Г.Роббинс Что такое математика? Глава VI, § 4

Л.Д.Кудрявцев Краткий курс математического анализа Главы 6, 7, 8

В.И.Смирнов Курс высшей математики т.1, Глава I, п.2, пп.34-44

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 2, §4, пп. 66-79

5.6.Производная и дифференциал

Понятие производной. Геометрический смысл производной

Дифференцируемость функции. Критерий дифференцируемости

Дифференциал. Геометрический смысл дифференциала. Связь дифференциала функции с производной

Свойства производных

Производные основных элементарных функций

Понятие локального экстремума

Теоремы Ролля, Лагранжа и Коши и их применение

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 10

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков Математика для психологов» Часть II, глава 1, 2

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 8

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава Х

Я.Б.Зельдович, И.М.Яглом Высшая математика для начинающих физиков и техников. Часть 1, глава 2 § 1-7, глава 4 § 1-12

А.Я.Хинчин 8 лекций по математическому анализу. Лекция V

В.И.Смирнов Курс высшей математики т.1, Глава II, п.3

Р.Курант, Г.Роббинс Что такое математика? Глава VIII, § 2, п. 1-8, § 2

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 3, § 1, пп. 90-102, § 2, пп. 103-108, § 3, пп. 109-114

Е.Титчмарш Теория функций, Глава 11

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 1, пп.10,11,12

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 3

Применение производных к исследованию функций

Построение графиков

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 11, пп.8-13

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 9, п.9.4

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XI, пп.7, 8, 10

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 4, § 1, пп. 131-140, § 2, пп. 141-145, § 3, пп. 146-149

Правила Лопиталя для раскрытия неопределенностей, их применение

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 11, п.4

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XI, п.п.1-3

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Глава 7, п.7.2

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 1, п.13

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 4, § 4, пп. 150-152

5.7.Интеграл

Первообразная. Неопределенный интеграл

Свойства неопределенного интеграла

Замена переменной в неопределенном интеграле. Интегрирование по частям

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 12

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Глава 5

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 10

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XIII

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 3, п.п. 28-31

В.И.Смирнов Курс высшей математики т.1, Глава III, п.8

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 2, глава 8, § 1, пп. 263-271, § 2, пп. 272-277, § 3, пп. 283-285

Определенный интеграл. Интегральные суммы

Геометрический смысл определенного интеграла. Вычисление площадей

Формула Ньютона-Лейбница

Условие интегрируемости

Свойства определенного интеграла. Интегрирование по частям и замена переменной в определенном интеграле

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 13

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Глава 3, 4

А.В.Дорофеева «Высшая математика. Гуманитарные специальности».Глава 11

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XIV

Я.Б.Зельдович, И.М.Яглом Высшая математика для начинающих физиков и техников

Часть 1, Глава 3 § 1-6, глава 5§ 1-6

А.Я.Хинчин 8 лекций по математическому анализу. Лекция VI

В.И.Смирнов Курс высшей математики т.1, Глава III, п.9

Р.Курант, Г.Роббинс Что такое математика? Дополнение к Главе VIII, § 1, п.2-3

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 2, глава 9, § 1, пп. 294-301, § 2, п. 306, § 3, пп. 309, 312, 313

Е.Титчмарш Теория функций, Глава 10

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 3, пп. 32-37

Интеграл с переменным верхним пределом

Понятие несобственного интеграла

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 13, п.8

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Глава 7

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 11, п.11.6

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» ГлаваXIV, п.2, п.12

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 2, глава 13, § 1, пп. 470-472, § 2, пп. 479-483

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 3 п.38

Функция Гаусса

Функция Лапласа

Интеграл Эйлера-Пуассона

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 12, п.1

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XXIV, п.4, глава XXV, Б, п.12,13

5.8.Функции нескольких переменных

Определение n-мерного пространства. Понятие функции нескольких переменных

Предел и непрерывность функций нескольких переменных

Частные производные. Дифференцируемость функций нескольких переменных

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 15, пп.1, 2, 3, 4, 5

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава ХХ, пп.1, 2, 3

Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления т. 1, глава 5, § 1, пп. 150-162, 164, 165, 167, § 2, пп. 169, 176-179, § 4, пп. 189, 193

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 9

В.И.Смирнов «Курс высшей математики», т.1, Глава V, п.15

Кратные интегралы. Повторные интегралы

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 16

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XXIV

Б.Гилбаум, Дж.Олмстед Контрпримеры в анализе Глава 10

Л.Д.Кудрявцев «Краткий курс математического анализа» Глава 5, пп. 42, 43

5.9. Ряды

Числовой ряд и его сумма

Необходимое условие сходимости

Признаки сходимости числовых рядов

Функциональные ряды

Ряды Тейлора

В.А.Ильин, А.В.Куркина «Высшая математика» Глава 17, пп.1-4

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 12

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XXI, пп.1-14

Л.Д.Кудрявцев Краткий курс математического анализа Глава 4

В.И.Смирнов Курс высшей математики т.1, глава IV, пп.12, 13

1.6. Элементы линейной алгебры

Системы линейных уравнений. Понятие матрицы. Матричная запись системы линейных уравнений. Системы двух и трех линейных уравнений. Система n линейных уравнений с n неизвестными

Действия с матрицами: линейные операции, умножение, транспонирование

Понятие обратной матрицы

Понятие определителя. Вычисление определителя матрицы 2×2 и 3×3

Вычисление определителя матрицы произвольного порядка

Правило Крамера. Метод Гаусса

Обратная матрица

Матричные уравнения

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть I, главы 1-4

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XVII

З.И.Боревич «Определители и матрицы»

Д.К.Фаддеев «Лекции по алгебре» Глава IV

Р.Курант «Курс дифференциального и интегрального исчисления» т 2, глава 1, § 3

Интернет-ресурсы

Сайт центра непрерывного математического образования http://www.mccme.ru

Образовательный портал Exponenta.ru http://www.exponenta.ru (разделы для преподавателей – лекции, раздел для студентов – рекомендации к решению задач, использование статистических пакетов при компьютерной обработке)