ОБЩИЕ И СПЕЦИАЛЬНЫЕ МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ, Учебное пособие

метки: Данные, Явление, Значение, Исследование, Метод, Результат, Рассмотреть, Ответ

СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЙ

(Учебное пособие)

Санкт-Петербург

Издательство РГПУ им. А.И.Герцена

Печатается по решению кафедры методики начального обучения математике и природоведению и РИСа РГПУ им. А.И.Герцена

Научный редактор канд. пед. наук, доц. М.И.Калинина

Рецензенты: доктор физ.-матем. наук, доц. Граничин О.Н. (СПбГУ), канд. пед. наук, доц. Сурикова С.В. (РГПУ).

Граничина О.А. СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЙ:Учебное пособие. – СПб.: Изд-во РГПУ им. А.И.Герцена,2002. – с.48; ил.

Данное пособие предназначено для студентов, изучающих специализированный курс «Математические методы психолого- педагогических исследований», а также для выпускников факультета начального образования, работающих над дипломной работой.

Пособие сжато излагает основные этапы статистических исследований, способы сбора, обработки и представления собранных экспериментальных данных.

... методов исследования. Одной из наиболее признанных и известных классификаций методов психолого-педагогического исследования является классификация, предложенная Б.Г. Ананьевым. Все методы он разделил на четыре группы: • организационные; • эмпирические; • по способу обработки данных; ...

ВВЕДЕНИЕ

Курс математических методов психолого-педагогических исследований призван способствовать формированию у студентов подлинного научного мировоззрения, способности глубже понять роль и место статистических закономерностей в научной картине мира, помочь лучше уяснить взаимосвязи естественно — научных предметов между собой и связь их с задачами предстоящей исследовательской деятельности (в частности, с задачами прогнозирования, а также обработки и анализа результатов научно-исследовательской работы).

В состав пособия включены следующие темы: детальное рассмотрение основных методов статистического исследования, понятие об основных методах количественной оценки педагогических исследований, методика разработки программы педагогического эксперимента, методика анализа данных педагогического эксперимента, а также представление о числовых характеристиках выборки.

Для успешного изучения этого курса студент должен, прежде всего, проверить свои знания по математике и теории вероятностей, полученные в школе и, в дальнейшем, в университетском курсе математики.

Статистические методы применяются при массовых наблюдениях явлений и вместе с тем они выявляют закономерности и порядок на основе имеющихся отдельных фактов, наблюдений и измерений. Строго говоря, математическая статистика- это наука о методах количественного анализа массовых явлений, учитывающая одновременно и качественное своеобразие этих явлений. Цель любой науки — познание общих закономерностей, позволяющее предвидеть течение явлений и выбирать рациональные пути поведения в типичных ситуациях. И это в полной мере относится и к математической статистике.

Первые работы по математической статистике относятся к XVIII в. и касались статистики народонаселения и вопросов страхования. Дальнейшее ее развитие было связано с созданием теории ошибок в конце XVIII — начале XIX в. А уже в XIX веке математическая статистика была выделена в самостоятельную науку, а толчком к этому послужили исследования в области биологии.

В задачах научных исследований наблюдения занимают очень важное место. Однако единичное наблюдение может нести много особенного, свойственного только данному объекту и не отражающее общую природу интересующего явления. Например, при изучении успеваемости учащихся данного класса нельзя сделать объективные выводы на основе данных об успеваемости отдельного ученика. Поэтому для получения общей закономерности необходимо проведение большого числа наблюдений. Наблюдения должны быть осуществлены с учетом многих обстоятельств и специальным образом организованы. Но зачастую, даже имея достаточное количество данных, можно прийти к неправильным выводам. И здесь возникает необходимость в изучении методов обработки полученных наблюдений. Эти методы и предлагает математическая статистика.

Заметим, что в каждой области человеческих знаний применяются свои статистические методы, выбор которых определяется характером изучаемых явлений. Данное пособие ориентировано на широкий круг исследователей, проводящих свои эксперименты в области психологии и педагогики, и потому здесь мы, в основном, ограничимся лишь рассмотрением тех статистических методов, которые используются в данных областях.

При составлении данного пособия автор использовал ценный материал, опубликованный в работах Ильиной Т.А., Павлова Ю.В., Озеран Л.Г., посвященных данной проблематике.

4 стр., 1802 слов

Методы эмпирического педагогического исследования: наблюдение

... перед собой определенной цели. Наблюдение как метод психолого-педагогического исследования предполагает постановку четкой, корректно сформулированной цели. ... или иных изучаемых явлений, процессов. Например, при исследовании трудоемкости учительской и ученической работы на уроке наблюдается ... поскольку в этом случае результаты обработки данных наблюдения не могут считаться достоверными. 3. ...

ОБЩИЕ И СПЕЦИАЛЬНЫЕ МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

При изучении педагогических явлений применяются различные методы исследования.

Метод — в самом общем значении- способ достижения цели, представляющий собой определенным образом упорядоченную деятельность. Для ведения педагогических исследований обычно применяется ряд общенаучных и специальных методов, рассматриваемых здесь в соответствии с двумя направлениями научного поиска, часто совпадающими с двумя этапами в научно-исследовательской работе. Речь идет о:

■ методах работы с литературой;

■ методах исследования реально существующего или специально организуемого практического опыта.

Как правило, исследование любой педагогической проблемы начинается с изучения литературы. Работа с литературными источниками предполагает использование таких общенаучных методов, как составление библиографии, аннотирование, реферирование, конспектирование, выписывание данных и цитат. Выбор метода работы с литературными источниками зависит от цели работы: некоторые книги и статьи внимательно изучаются, другие — просто прочитываются, третьи — лишь просматриваются.

Библиография — перечень литературных источников, отобранных для работы в связи с исследуемой проблемой. В случае наличия в библиотеке значительного числа работ по проблеме отбирается литература с учетом года издания, авторитетности, известности в науке автора, издательства, общей направленности работы (определяемой пока по заглавию).

Решение о том, как работать с литературным источником, принимается уже после непосредственного ознакомления с книгой или статьей.

Общее содержание ее может найти отражение в краткой записи- аннотации, дающей общее представление о поднимаемых в работе вопросах, или в реферате— сжатом переложении основного содержания работы.

Конспектирование предполагает ведение достаточно подробных записей. Проводится оно для вычленения главных идей и положений, развиваемых в работе. В ряде случаев представляется необходимым сделать лишь отдельные выписки фактических или цифровых данных или цитат, дословных выражений или определений, даваемых самим автором.

Все виды работы с книгой требуют очень четкого оформления основных данных: обязательной записи фамилии и инициалов автора, названия работы, издательства (или для статьи- названия журнала, газеты), места и года издания (для периодики- номера журнала или даты опубликования в газете).

Изучение литературы (всех ее видов или только части их) необходимо для более четкого представления методологии исследования и определения общих теоретических позиций, а также выявления степени научной разработанности данной проблемы. Всегда важно выявить, насколько и как эта проблема освещена в общих научных трудах и специальных работах по данному вопросу, отражающих результаты соответствующих исследований. Исследователь при этом узнает, какие стороны проблемы уже достаточно хорошо разработаны, по каким вопросам ведутся научные споры, сталкиваются разные научные концепции и идеи, что уже устарело, какие вопросы еще не решены, и на основании этого определяет область своего исследования. Изучение литературы, описывающей тот или иной опыт, вооружает исследователя также некоторыми конкретными данными, научными фактами.

4 стр., 1691 слов

изучение методов диагностики и коррекции развития графомоторных ...

... формированию графомоторных навыков у детей с дизартрией. Методы исследования - изучение и анализ научной литературы. Структура курсовой работы: курсовая работа состоит из: введения, 2 теоретических глав, ... логопедии, психологии, педагогики и медицины. Информационную базу данной курсовой работы составляют следующие научные источники: данные и сведения из книг, журнальных статей, научных докла ...

Огромное значение для решения большинства проблем педагогики имеет изучение реально складывающегося учебно-воспитательного процесса, теоретическое осмысление и переработка творческих находок практических работников, обобщение и пропаганда передового опыта. В этих целях применяются такие методы, как наблюдение, беседа, анкетирование, изучение письменных графических и творческих работ обучаемых, педагогической документации.

Наблюдение представляет собой целенаправленное восприятие какого-либо педагогического явления, с помощью которого исследователь вооружается конкретным фактическим материалом или данными. Для того, чтобы внимание исследователя не рассеивалось и было сосредоточено, прежде всего, на особо интересующих его сторонах наблюдаемого явления, заранее очень тщательно разрабатывается программа наблюдения, четко выделяются объекты наблюдения, предусматриваются способы регистрации тех или иных ожидаемых событий. Часто наблюдение дополняется беседой.

Беседа применяется как самостоятельный метод или как дополнительный в целях получения дополнительной информации или разъяснений по поводу того, что не было достаточно ясным при наблюдении. Она также проводится по заранее намеченному плану с выделением вопросов, подлежащих выявлению. Беседа ведется в свободной форме без записи ответов собеседника в отличие от интервьюирования (разновидности метода беседы), перенесенного в педагогику из социологии. При интервьюировании исследователь строго придерживается заранее намеченных вопросов, задаваемых в определенной последовательности. Ответы при этом открыто записываются.

При анкетировании — методе массового сбора информации с помощью анкет — ответы на вопросы записывают те, кому адресованы анкеты. Как правило, анкетирование применяется на заключительном этапе исследования и имеет целью получение таких данных, которые исследователь не может получить другим путем.

Эффективность беседы, интервьюирования, анкетирования — трех основных методов выявления суждений, отношений, оценок и сбора другого интересующего исследователя фактического материала — во многом зависит от содержания и формы задаваемых вопросов, тактичного объяснения их цели и назначения. В частности, рекомендуется, чтобы вопросы были посильными, однозначными, краткими, ясными, объективными, т.е. не содержали бы в скрытом виде внушения, вызывали бы интерес и желание отвечать и т.п.

Другой метод сбора фактических данных — изучение педагогической документации, характеризующей учебно-воспитательный процесс в том или ином учебном заведении (журналов учета успеваемости, посещаемости, личных дел и медицинских карт обучаемых и т.д.).

В этих документах зафиксированы многие объективные данные, помогающие установить ряд характеристик, причинные связи, выявить некоторые зависимости. Изучение письменных, графических творческих работ обучаемых является методом, вооружающим исследователя ценными данными, характеризующими индивидуальность каждого обучаемого, его отношение к работе, наличие тех или иных способностей.

23 стр., 11371 слов

Педагогическая психология 10

... Для воспитателя цели и мотивы – это, прежде всего, цели и мотивы педагогической деятельности и педагогического общения. Для воспитанников - это цели тех конкретных видов деятельности, в ... с конкретными видами деятельности и ситуациями) свойственны и воспитателям, но имеют подчиненный педагогическим целям и потребностям характер, если воспитатель ведет себя профессионально. Успешность воспитания ...

Наиболее важный этап в работе с применением указанных выше методов — анализ и научная интерпретация собранных данных, умение исследователя от конкретных фактов перейти к более общим выводам, а в некоторых случаях даже дать прогноз развития интересующего его процесса.

Однако для того, чтобы судить об эффективности тех или иных педагогических взаимодействий или ценности методических находок, сделанных практическими работниками, а тем более для того, чтобы давать какие-либо рекомендации относительно применения тех или иных нововведений в массовой практике, рассмотренных методов недостаточно, так как они улавливают в основном лишь чисто внешние связи между отдельными сторонами изучаемого педагогического явления.

Поэтому значительное внимание уделяется педагогическому эксперименту — специальным образом организованной проверке того или иного метода или приема для определения его эффективности. В отличие от изучения реально сложившегося опыта с применением методов, регистрирующих лишь то, что уже существует, эксперимент всегда предполагает создание нового опыта, в котором активную роль должно играть предполагаемое и проверяемое нововведение.

Необходимость в эксперименте возникает тогда, когда учеными выдвигается какая-либо новая идея или предположение, требующее проверки, или же тогда, когда необходимо научно проверить интересный опыт, педагогические находки практиков, подмеченные и выделенные исследователем, дать им объективную оценку. Эксперимент необходим и тогда, когда нужно проверить разные точки зрения или суждения по поводу одного и того же педагогического явления или метода, уже подвергавшегося проверке, сопоставить их результаты и сделать выводы о том, какие из них более доказательны. Нужен от и тогда, когда необходимо найти наиболее рациональные и эффективные пути внедрения в практику обязательного или признанного положения, указания, постановления.

Одно из основных условий применения педагогического эксперимента в школе — проведение его без нарушения нормального хода учебного процесса, когда есть достаточно оснований полагать, что проверяемое нововведение может способствовать повышению эффективности обучения и воспитания или хотя бы не вызовет нежелательных последствий. Такой эксперимент называется естественным экспериментом.

Научно обоснованное предположение о возможной эффективности того или иного проверяемого экспериментально нововведения называется научной гипотезой. Таким образом, ясно, что в основе педагогического эксперимента всегда лежит научная гипотеза, а сам эксперимент проводится с целью ее проверки. Если она выведена лишь на основании теоретического анализа и рассуждений и не имеет пока опоры в реальном опыте, то создание этого опыта в соответствии с выдвигаемым теоретическим положением может быть названо созидающим экспериментом.

Первый этап эксперимента, когда изучается лишь общая реакция обучаемых на нововведение, а также выявляется отношение к исследованию преподавателя, называется поисковым или разведывательным экспериментом. Иногда его еще называют констатирующим экспериментом. В ходе констатирующего эксперимента исследователь также выявляет уровень овладения обучаемыми теми разделами программы, на которые он будет опираться в ходе проведения экспериментальной работы.

3 стр., 1241 слов

Темы курсовых работ по дисциплине «Социальная психология малых групп»

... ответа или ответов. Проводимый эксперимент приобретает конкретный смысл лишь тогда, когда его результаты направлены на проверку выдвинутой гипотезы. Кроме того, экспериментальные работы нуждаются в четком определе ... брошюруются. На титульном листе помещаются название института, тема работы, данные об авторе, факультете и группе. Затем идет план работы из трех-четырех вопросов, отражающих тему в ...

По получении предварительных данных, подтверждающих вероятность и обоснованность выдвигаемой гипотезы, возможно проведение сравнительного эксперимента, т.е. такого эксперимента, когда в одном классе ( или с одной группой обучаемых) работа проводится с применением нового метода, а в другом — при прочих примерно равных условиях- работа ведется как обычно.

Данные сравнительного эксперимента могут считаться надежными лишь тогда, когда обеспечена максимальная эквивалентность условий работы с обучаемыми обеих групп. Например, занятия ведутся одним преподавателем, в ту же смену, класс или группа примерно одинакового состава по успеваемости и другим показателем, характеризующим познавательные процессы и т.п. Различными должны быть лишь сравниваемые методы или приемы работы.

Существенную часть эксперимента составляет наблюдение, проводимое по специально разработанной программе, а также сбор определенных данных, для чего применяются контрольные работы, анкеты, беседа и т.д. В последнее время невозможно себе представить педагогическое исследование без привлечения технических средств, особое место среди которых занимает компьютер.

Очень важен в научном отношении этап анализа собранных данных, их теоретического осмысления и обобщения. На этом этапе экспериментатор старается отделить случайное и частное от необходимого и существенного, стремясь обнаружить регулярность или порядок, которому следует целая масса индивидуальных случаев, вскрыть внутренние связи между ними, установить некоторую закономерность. При проведении такого анализа исследователь задумывается, прежде всего, о том, какова причинно-следственная зависимость между применяемыми методами или приемами воздействия и получаемыми результатами. В ходе анализа данных экспериментатор также ищет причины, объясняющие появление некоторых неожиданных, непредвиденных результатов, определяет условия, при которых наступало то или иное явление, стремится отделить то специфическое, что могло оказать влияние лишь в данном конкретном случае и что нетипично для других и т.п. Для проведения анализа данных и их интерпретации составляются таблицы, вычерчиваются диаграммы, графики, кривые зависимостей. Об этом подробно пойдет речь далее.

СУЩНОСТЬ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ПЕДАГОГИЧЕСКИХ ЯВЛЕНИЙ

В последнее время предпринимаются серьезные шаги, направленные на внедрение в педагогику кибернетических и математических методов оценки и измерения педагогических явлений и установления количественных зависимостей между ними. Кибернетические и математические методы позволяют подойти к решению одной из сложнейших задач педагогики — количественной оценки педагогических явлений. Лишь обработка количественных данных и полученные при этом выводы могут объективно доказать или опровергнуть выдвинутую гипотезу.

При организации любого измерения всегда предполагается соотнесение (сравнение) измеряемого с измерителем (эталоном).

После процедуры соотнесения (сравнения) производится оценка результата измерения. Если в технике в качестве измерителей используют, как правило, материальные эталоны, то в социальных измерениях, в том числе при педагогических и психологических измерениях, измерители могут быть идеальными. Действительно, чтобы определить сформировано или не сформировано у обучаемого конкретное умственное действие, необходимо сравнить действительное с необходимым. В этом случае, необходимое- это идеальная модель, существующая в голове учителя.

Следует заметить, что только некоторые педагогические явления могут быть замерены. Большинство же педагогических явлений не поддаются измерению, поскольку отсутствуют эталоны педагогических явлений, без которых не может быть выполнено измерение.

Что касается таких явлений, как активность, бодрость, пассивность, усталость, умения, навыки и т.д.., их измерить пока не представляется возможным, поскольку нет эталонов активности, пассивности, бодрости и т.д. Ввиду чрезвычайной сложности и, в большей части, практической невозможности измерения педагогических явлений в настоящее время применяются специальные методы приближенной количественной оценки этих явлений.

Широко известны следующие два метода приближенной количественной оценки педагогических явлений: метод регистрации и ранговый метод, о которых подробно говорится ниже.

В настоящее время принято все психолого-педагогические явления подразделять на две большие категории: объективные материальные явления (явления, существующие вне и независимо от нашего сознания) и субъективные нематериальные явления (явления, свойственные данному лицу).

К объективным материальным явлениям относятся: химические и биологические процессы, движения, совершаемые человеком, издаваемые им звуки, выполняемые им действия и т.д.

К субъективным нематериальным явлениям и процессам относятся: ощущения, восприятия и представления, фантазии и мышление, чувства, влечения и желания, мотивация, знания, умения и навыки и т.д.

Все признаки объективных материальных явлений и процессов наблюдаемы и могут быть, в принципе, всегда измерены, хотя современная наука подчас не в состоянии это сделать. Любое свойство или признак может быть измерено непосредственно. Это значит, что его путем физических операций всегда можно сравнить с некоторой реальной величиной, принятой за эталон меры соответствующего свойства или признака.

Субъективные нематериальные явления нельзя измерить, поскольку для них нет и не может быть материальных эталонов. Поэтому здесь используются приближенные методы оценки явлений — различные косвенные показатели.

Суть применения косвенных показателей заключается в том, что измеряемое свойство или признак изучаемого явления связывают с определенными материальными свойствами, а величину этих материальных свойств принимают за показатель соответствующих нематериальных явлений. Например, эффективность нового метода обучения оценивают успеваемостью учащихся, качество работы ученика — количеством допущенных ошибок, трудность изучаемого материала- величиной затраченного времени, развитие психических или нравственных черт- числом соответствующих поступков или проступков и т.д.

При всем том большом интересе, который исследователи обычно проявляют к методам количественного анализа экспериментальных данных и массового материала, полученного с помощью разных методов, существенным является этап обработки — их качественный анализ. С помощью количественных методов можно с той или иной степенью надежности выявить преимущество того или иного метода или обнаружить общую тенденцию, доказать, что проверяемое научное предположение оправдалось и т.д. Однако качественный анализ должен дать ответ на вопрос, почему это произошло, что этому благоприятствовало, а что служило помехой, и насколько существенно влияние этих помех, не слишком ли специфичны были условия проведения эксперимента для того, чтобы данная методика могла быть рекомендована для использования в иных условиях и т.д. На этом этапе важен и анализ причин, побудивших отдельных опрашиваемых дать негативный ответ, и выявление причин тех или иных типовых и даже случайных ошибок в работах отдельных учащихся и т.д. Применение всех этих методов анализа собранных данных помогает более точно оценить результаты эксперимента, повышает надежность выводов о них и дает больше оснований для дальнейших теоретических обобщений.

Самое важное в завершенном педагогическом исследовании — внедрение его результатов в практику. Под внедрением результатов может пониматься широкое информирование педагогической общественности о полученных выводах, или выявленных закономерностях, дающих основание для внесения каких-либо изменений в практику; создание новых учебных и методических пособий, базирующихся на полученных данных экспериментального исследования; разработка методических инструкций и рекомендаций и т.д. При этом, если подтверждается эффективность и действенность каких-либо педагогических находок практиков, их опыт пропагандируется, показывается возможность переноса его в иные условия.

МЕТОДИКА РАЗРАБОТКИ ПРОГРАММЫ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА

Рассмотрим последовательно основные действия исследователя, приступающего к разработке программы экспериментальной части своей работы:

А) прежде всего, необходимо решить вопрос о необходимости этой экспериментальной части;

Б) далее решается вопрос о выдвижении научной гипотезы, которая должна быть положена в основу эксперимента; гипотеза называется научной и должна быть научной потому, что, хотя она и может содержать элемент догадки, интуитивной веры в возможный положительный эффект, она должна базироваться на определенных научных данных, подкрепляться теоретическими доводами или умозаключениями;

В) следует продумать вопрос о том, какие потребуется применять виды эксперимента; решение вопроса о видах и типах эксперимента зависит от ряда моментов: от цели и конкретной задачи исследования, этапа работы исследователя над проблемой, используемых средствах над решением проблемы и т.д;

Г) планирование эксперимента далее включает в себя также выбор и оценку общих условий его проведения: средства для его ведения, место для его проведения, обучаемые, преподаватель;

Д) особо следует выделить оценку и правильный отбор уравниваемых и варьируемых условий эксперимента.

Уравниваемыми условиями проведения эксперимента называются условия, обеспечивающие сходство и неизменность протекания эксперимента в контрольных и экспериментальных классах. К уравниваемым условиям обычно относятся: состав обучаемых (примерно одинаковый в экспериментальных и контрольных классах или группах); учитель (один и тот же учитель ведет занятия в экспериментальных и контрольных группах); учебный материал (одинаковый круг вопросов, равный объем); равные условия работы (одна смена, примерно одинаковый порядок следования занятий по расписанию и т.д).Правда, известный психолог Л.В.Занков считает, что уравнивание состава нереально, что это методологически ложно и практически недостижимо. Поэтому на практике, как правило, отбираются группы примерно равные по общей успеваемости. В случае же, если в условиях данного учебного заведения нельзя подобрать две примерно равные по этим показателям группы, в качестве экспериментальной принято брать группу с более низкой успеваемостью: в случае получения положительных результатов в итоге экспериментальной работы эти результаты будут более убедительными. Что касается уравнивания условий, связанных с преподавателем, то во всех случаях желательно, чтобы занятия и в контрольной и в экспериментальной группах вел один и тот же преподаватель или сам экспериментатор. Ведение занятий в разных группах разными учителями при сравнительном эксперименте не допускается, так как личность учителя, его умение установить его контакт с учениками, применяемые им методы воздействия на учащихся представляют собой такие характеристики, которые никогда не могут быть уравнены. В отдельных случаях, особенно на первом этапе исследовательской работы или тогда, когда идет опробование учебного материала, эксперимент можно вести в одной группе на разном, но однородном материале, применяя в работе с ним различные методы. В этом случае уравниваемыми условиями будут: группа (одна и та же), преподаватель (один и тот же), учебный материал (однородный, одинаковой степени трудности).

Подобное проведение эксперимента может иметь место и в том случае, если не удается добиться примерного уравнивания состава обучаемых или обучения в обеих группах одним учителем. Неполное сходство учебного материала в этом случае будет иметь меньше влияния, нежели сильные различия в первых двух характеристиках.

Перейдем теперь к рассмотрению вопроса о варьируемых условиях. Классический принцип проведения экспериментального исследования исходит из предположения о том, что в ходе эксперимента меняется – варьируется — лишь одна переменная при сохранении постоянными всех остальных. Варьируемыми условиями называются точно определяемые и сопоставимые условия, подлежащие изменению с целью экспериментального сравнения с аналогичными условиями в контрольных группах. Самое основное в этой работе — точное и четкое выделение того, что подлежит экспериментальной проверке и сравнению.

Составление собственно программы эксперимента включает в себя общую часть, связанную с постановкой конкретных задач, гипотез, определением методов получения экспериментальных данных, и частные программы работы участников эксперимента: учителя (или самого экспериментатора), ведущего занятия как в экспериментальном, так и в контрольном классах, наблюдателя или помощника, ведущего наблюдения, делающего по ходу занятия необходимые отметки.

Подобное распределение обязанностей между экспериментатором, его помощниками и учителем является практически важным, так как одному человеку не под силу осуществление программы наблюдения и одновременное ведение занятий. Правда, в ряде случаев экспериментатор, ведущий занятие, может также осуществлять плановое наблюдение за работой отдельных учащихся — специально подходить к заранее намеченным лицам, проверять, как у них идет работа, интересоваться тем, какие они встречают трудности в работе и т.д.

Общие задачи и методика организации эксперимента должны найти отражение в развернутом плане-программе эксперимента, куда могут быть занесены основные необходимые экспериментатору данные.

МЕТОДИКА АНАЛИЗА ДАННЫХ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА

Анализ и обработка протоколов наблюдений

Протоколы наблюдений и хронометрирование занятий обычно представляют собой текстовую запись, воспроизводящую полностью или частично ход проведенного занятия. В ряде случаев, когда наблюдатель производит выборочное наблюдение за отдельными учащимися или фиксирует лишь отдельные интересующие его моменты, у него оказывается заполненной та или иная таблица, составленная в соответствии с целью проводившихся наблюдений. Чаще же всего экспериментатору при изучении общих записей, сделанных по ходу ведения занятий, приходится извлекать из них необходимую ему информацию, которую полезно для наглядности также оформлять в виде таблицы.

Не существует строгих регламентаций по работе с протоколами наблюдений, они должны лишь служить примерным ориентиром в этой работе. Самое важное при работе с протоколами и другими видами записи наблюдавшегося реального учебного процесса — уметь выделить данные, содержащие определенную информацию, найти причины тех или иных особенностей работы обучаемых на том или ином этапе работы над учебным материалом.

Анализ данных беседы

Очень часто в ходе наблюдения за проведенным занятием у экспериментатора (или наблюдателя) могут возникнуть вопросы, связанные с содержанием работы, уточнением отдельных моментов организации работы, выявлением отношения обучаемых к тому или иному виду работы, оценку ими трудностей, возникающих в ходе проведения работы. Беседа проводится экспериментатором, прежде всего, с целью получить необходимые разъяснения, уточнить записи, сделанные на занятии, проверить свои впечатления и т.п. Часто беседа проводится и с учениками, и с учителями по заранее разработанной программе, в которую включаются вопросы, интересующие экспериментатора. Особое значение имеют данные, сообщенные в ходе беседы учителем, участвующим в эксперименте, проводившим занятие по предложенной ему методике.

В случае положительной оценки экспериментатор получает, таким образом, подтверждение своего замысла, укрепляется его вера в то предположение (гипотезу), на котором основывается эксперимент. В случае отрицательных суждений или отдельных замечаний очень важно знать общее отношение учителя к предложенной ему методике — не был ли он уже заранее настроен против, проявлял ли готовность выполнить план-программу ведения занятий, разработанную экспериментатором. В любом случае все замечания должны быть тщательно записаны, изучены и обдуманы. Следует отметить, что замечания предубежденного учителя имеют особую ценность, так как он скорее увидит слабые места или недоработки в новой методике, нежели увлеченный данной идеей учитель-энтузиаст, сам горячо стремящийся к успеху.

Анализ результатов беседы (или отзыв) можно оформить в виде рабочей таблицы такого примерно вида:

Положительные моменты	Недостатки	Выводы
…	…	…

Анализ ответов на вопросы анкеты

Если беседа имеет ценность непосредственного общения и обеспечивает немедленное получение ответов на интересующие экспериментатора вопросы, то анкеты дают возможность собрать значительный массовый материал.

Поскольку с помощью анкет можно собрать большой материал, он требует и количественной обработки, и проведения тщательного качественного анализа.

Количественная обработка может дать, прежде всего, общие данные о количестве утвердительных и отрицательных ответов, полученных по каждому вопросу анкеты. (При большом количестве ответов можно перевести эти данные в проценты).

Количественный анализ должен быть направлен в первую очередь на анализ негативных суждений (выявление их причины и принятие решений о необходимости изменения тех или иных частей программы).

Положительные же суждения используются как материал, подтверждающий гипотезу.

При проведении экспериментальной проверки в разных местах большую наглядность этим данным придает сведение их в общие таблицы: в этих случаях виднее становятся совпадения данных (легче обнаружить тенденцию), а также разброс отдельных данных, который носит случайный характер или объясняется какими-либо причинами, характерными лишь для данных условий проведения эксперимента.

Таким образом, общая методика обработки анкетных данных сводится к их тщательному подсчету, проведению внимательного анализа всех случаев заметного совпадения, разнобоя в данных, разброса. Анкетные данные могут помочь выявлению возможных причин дачи разнородных ответов и более четко проявляющихся тенденций, которые могут указывать на определенную закономерность, связанную как с особенностями восприятия учащихся, так и с особенностями предлагаемой методики или организацией занятий с учащимися.

Анализ результатов контрольных работ

Особое значение имеет сбор и интерпретация данных, полученных на контрольных работах (текущих, итоговых, отсроченных).

Для экспериментатора огромное значение имеет количественный и качественный анализ всех допущенных обучаемыми ошибок. Надежность и информативность этих данных во многом зависит от того, что и как проверялось, т.е. адекватны ли контрольные вопросы и задания содержанию, целям и задачам обучения, так ли они поставлены, то ли они выявляют, что действительно может случить показателем усвоения знаний. Поскольку это действительно вопрос, представляющий весь смысл проверки качеств усвоения, остановимся очень кратко на некоторых основных положениях, связанных с методикой проведения контрольных работ.

В настоящее время очень распространено выделение в учебном материале небольших единиц, усвоение которых затем проверяется дифференцированно в зависимости от их значимости и весомости. Такими единицами могут быть новые понятия, вводившиеся в процессе изучения темы или раздела, по которому дается контрольная работа, отдельные умения или навыки, формирующиеся при изучении данной части учебного материала. Необходимо отметить, что для осуществления правильного подбора заданий, проверяющих действительное усвоение самого главного и существенного, важно проведение предварительной оценки каждой из выделенных единиц учебной информации. Эта оценка производится с учетом их значимости и весомости в общей системе знаний, умений и навыков по данной учебной дисциплине.

Эта значимость определяется с точки зрения: а) значения для усвоения последующих тем и разделов курса или других, связанных с ним, курсов; б) практического значения; в) содержащихся в них трудностей для усвоения.

В результате каждой из единиц может быть дана соответствующая ориентировочная оценка, относящая их к определенной категории, т.е. это могут быть единицы, знание которых: абсолютно необходимо (1), полезно и необходимо (2), полезно, но не существенно необходимо (3).

Естественно, при контроле главное внимание должно быть обращено на проверку усвоения единиц знаний, относимых к 1 и 2 категориям. Ряд исследователей вводят числовые коэффициенты- «веса» заданий, соответствующих важности значимости проверяемых с их помощью знаний, которые затем учитываются при подсчете числовых характеристик правильных и неправильных ответов. Если такие «веса» не вводятся, должна быть соблюдена определенная пропорция в количестве заданий, проверяющих более значимый материал. Для большей надежности проверки знаний можно вообще не давать заданий на проверку усвоения второстепенного по значимости учебного материала, выявляя усвоение единиц учебной информации, отнесенных лишь к 1 и 2 категориям.

При сборе массовых данных контроля при эксперименте большое значение имеет и форма, в которой даются контрольные задания. При ограниченном числе испытуемых задания, направленные на проверку усвоения самого основного и существенного, могут даваться в любой форме, т.е. могут требовать развернутых ответов, обоснований и т.п. При сборе массового материала большой популярностью пользуются тесты или задания тестового типа, т.е. требующие или очень краткого ответа, или выбора ответа из числа данных. При проведении контрольных работ-тестов возможно использовать некоторые простейшие приспособления для убыстрения подсчета числа правильных или неправильных ответов (например, разного рода шаблоны, проверки по «ключу»), однако неоценимую помощь в этом могут оказать средства вычислительной техники. Кроме того, благодаря сокращению времени, затрачиваемого на запись ответа, можно за единицу времени дать больше заданий, с помощью которых можно глубже и полнее проверить усвоение знаний, охватить разные их связи и зависимости. Значение имеет, конечно, как сама формулировка задания, так и подбор вариантов, предлагаемых на выбор. Необходимо учитывать, что в числе вариантов ответов, даваемых на выбор, не должно быть абсурдных, нелепых, нелогичных ответов, ответов, содержащих ложную информацию, которая может непроизвольно остаться в памяти учащегося. Важно также проверить, чтобы формулировки контрольных заданий соответствовали в основном формулировкам заданий в упражнениях, чтобы в них не было ничего неожиданного для обучаемых.

Таким образом, при подборе контрольных заданий экспериментатор исходит из того, что задания должны проверять усвоение самого существенного и значимого в изученном материале, быть нацеленными на выявление определенных аспектов и характеристик знаний, умений и навыков (в соответствии с выбранными критериями) и при использовании методики тестового контроля должны соответствовать основным требованиям к подбору вариантов ответов, предлагаемых на выбор.

Методика анализа ошибок.

Огромное значение для выявления рассмотренных выше показателей и характеристик усвоенных знаний и сформулированных умений и навыков имеет работа по анализу ошибок, допускаемых учащимися в контрольных работах. При правильном подборе и заранее продуманной нацеленности заданий некоторые характеристики выявляются сразу же при изучении ответов, данных на соответствующую группу вопросов (например, имеющих целью выявить объем знаний, прочность, осмысленность и т.д.).

Количество ошибок служит важным показателем для выявления как качества усвоения знаний, так и эффективности предлагаемой методики. Например, отсутствие ошибок в ответах на определенные задания может свидетельствовать не только о хороших знаниях обучаемых, но и служить сигналом о том, что задания — слишком легкие. Отдельные ошибки чаще всего носят случайный характер, но могут свидетельствовать о каких-либо пробелах в знаниях тех или иных учащихся, а также о каких-либо характерных особенностях протекания у них различных познавательных процессов.

Появление ошибок в ответах по тому или иному вопросу у многих обучаемых свидетельствует о какой-то закономерности, причиной появления которой может служить: недостаточная проработанность учебного материала; неточности в формулировке заданий; нечеткость исходных данных или даже какие-либо технические причины (опечатки, пропуск знака и т.д.).

В ряде случаев ошибки могут быть вызваны особенностями психологии восприятия или других психических процессов, связанных с познавательной деятельностью обучаемых. Приведем примеры некоторых типовых ошибок с указанием причины их появления.

Так, встречаются ошибки привычности. Например, при переходе от сложения к умножению может иметь место сложение множителей: 3+2=5 и 7ּ5=12. Ошибки устойчивости проявляются в повторении или добавлении ранее встречающейся буквы, цифры. Например, 7+9=19. Распространены ошибки сходства, проявляющиеся в неумении дифференцировать сходные буквы, знаки. Например, путают буквы ъ и ь, знаки ⋂ и ⋃ и т.д. Эти последние ошибки во многом проистекают и от методики обучения. Важно также предупредить появление и всех других ошибок, которые связаны с каким-либо интерферирующим влиянием, например, влиянием предшествующих знаний. Например, «family» в английском языке означает «семья», а не «фамилия», как в русском языке.

При анализе ошибок, особенно при заданиях с выбором ответа, часть ошибок может объясняться осторожностью, например, если вообще не выбран ни один вариант ответа. Пропуск заданий может, однако, свидетельствовать и о недостаче времени (задание было пропущено, чтобы потом над ним подумать, а времени не хватило).

Невыполнение последних заданий довольно часто говорит именно о нехватке времени, отведенного на выполнение контрольной работы.

При заданиях с выбором ответа имеется всегда и элемент случайности, риска (угадал — не угадал).

Общая же методика анализа ошибок при сборе массового материала складывается из выполнения следующих действий:

— производится общий подсчет количества ошибок по каждому вопросу;

— выделяются задания: а) в ответах на которые было допущено очень мало ошибок (или вообще не было ошибок); б) были лишь отдельные ошибки; в) было много ошибок; г) которые не были выполнены большинством обучаемых;

— по выявленным группам заданий проводится анализ возможных причин появления ошибок, которые могут носить частно — методический характер (быть связанными с недостатками методики объяснения и закрепления конкретного учебного материла); могут проистекать от недостатков предлагаемой методики; носить психологический характер; быть чисто случайными;

— делаются педагогические и методические выводы, направленные на внесение соответствующих изменений в структуру предлагаемой системы занятий по формированию того или иного знания.

ОСНОВНЫЕ МЕТОДЫ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ПЕДАГОГИЧЕСКИХ ЯВЛЕНИЙ

Ранее было сказано о том, что одна из важнейших задач, которую ставит перед собой педагог-исследователь, — получение количественных оценок педагогических явлений.

Рассмотрим методы, которые получили широкое распространение в педагогических исследованиях.

П. 1 Метод регистрации

Суть метода регистрации заключается в приписывании определенных чисел объектам, различающимся по некоторому, интересующему исследователя признаку. Например, выделяют какой-нибудь признак и отмечают каждый случай, когда в наблюдении или эксперименте встречается объект или явление с этим признаком. Каждому такому объекту или явлению приписывается «1». Каждому из наблюдаемых объектов или явлений, у которых этот признак отсутствует, приписывают «0».

Чтобы произвести регистрацию предметов или явлений, достаточно уметь отличать предметы или явления, имеющие данный признак, от предметов и явлений, у которых он отсутствует.

Такая регистрация дает меру для определения величин, характеризующих исследуемые явления.

Например, регистрируя в классе каждого неуспевающего ученика, получают число неуспевающих учащихся в классе, регистрируя каждый неуважительный пропуск занятий, получают число прогулов за соответствующий период времени, фиксируя каждое нарушение дисциплины учеником, получают общее число совершенных нарушений и т.д.

Из этих примеров следует, что с помощью метода регистрации можно числено оценить такие признаки, как успеваемость, посещаемость, дисциплинированность и т.д.

Таким образом, метод регистрации не требует знаний каких-либо количественных эталонов. В его основе лежит операция не физическая (измерение), а логическая, т.е. определение принадлежности данного объекта к некоторому классу с заданным признаком. Это очень важная особенность. Она позволяет осуществлять измерение даже тогда, когда невозможно количественно определить сами свойства изучаемых явлений.

С такой ситуацией педагог-исследователь сталкивается очень часто. Например, при изучении всех нематериальных педагогических явлений и процессов. Вот почему метод регистрации является одним из наиболее доступных и широко применяемых педагогами способов количественной оценки процессов обучения и воспитания. Это также объясняется еще и тем, что современный уровень педагогической науки пока не позволяет прямо измерить количество знаний, умений и навыков, уровень развития тех или иных нравственных качеств и т.д. Но, регистрируя ошибки, которые допускают в письменных работах ученики, поступки, которые они совершают и т.п. можно определить косвенные количественные характеристики всех этих признаков. А это значит, что можно строго математически исследовать закономерность учебного процесса.

При этом методе числа, которые получаются в качестве количественных характеристик интересующего нас педагогического явления, можно складывать и делить.

Из самой сущности метода регистрации вытекают и граничные условия его применимости.

Необходимым и достаточным условием такой оценки является условие наличия точного критерия, пользуясь которым, исследователь в любой ситуации может однозначно отличить объект, имеющий данный признак, от объекта, который этого признака не имеет.

Критерий должен точно и однозначно характеризовать признак, который мы собираемся регистрировать. Необходимо точное предварительное описание (определение) тех показателей признака, по которым мы будем устанавливать, имеется ли данный признак у данного объекта или нет.

Так, например, нельзя браться за подсчет количества успевающих учеников в классе, пока не условились, кого из учащихся считать успевающим, пока не установили совершенно четко, как будем отличать успевающего ученика от неуспевающего.

Одна из распространенных ошибок педагогов-исследователей заключается в том, что, проводя количественные исследования, авторы даже не пытаются сформулировать подобные критерии. А это приводит к тому, что полученные разными исследователями числовые данные нельзя сопоставлять, поскольку они получены при разных условиях.

П.2 Метод ранговой оценки.

Важное место в педагогических исследованиях занимает ранговый метод оценки педагогических явлений. Ранговой оценкой пользуются в тех случаях, когда величину признака измерить не представляется возможным и в тех случаях, когда мы не знаем, что представляет собой эта величина.

Суть метода ранговой оценки заключается в том, что явления или объекты располагаются в порядке возрастания или убывания величины рассматриваемого признака. Затем каждому объекту или явлению приписывается порядковое число, обозначающее его место в данном ряду. Это число называют рангом.

Ранговые числа подбирают так, чтобы объектам с большей величиной изучаемого признака приписывались числа большие, чем у объектов с меньшей величиной этого признака. При этом расстояние между значениями соседних рангов может быть произвольно (это определяет сам исследователь).

Примером ранговой оценки может служить оценка работ и ответов учащихся по пятибалльной шкале.

Приведем пример применения метода ранговой оценки педагогического явления.

П р и м е р 1. Группа учащихся выполняла контрольную работу. Каждый из учащихся должен был ответить на 10 вопросов. Оценка ответов проводилась по пятибалльной шкале следующим образом:

число правильных ответов: 1 2 3 4 5 6 7 8 9 10

оценка в баллах: 2 3 4 5

Следует заметить, что любой ряд чисел, написанный в возрастающем порядке, был бы пригоден, т.к. нулевая точка отсчета и интервалы между двумя соседними цифрами в порядковых измерения неизвестны.

Эти цифры дают ранговую оценку знаний ученика по данной контрольной работе, разделу, курсу и т.д., а не объем знаний.

Ранговая оценка показывает только положение ученика среди других учеников, например, по признаку успеваемости. Но она не определяет величины самого интервала, на которые разбита вся последовательность возможных значений величины признака, поскольку эта разбивка делается произвольно.

Если вернуться к нашему примеру, то нетрудно заметить, что неудовлетворительная оценка охватывает шесть интервалов признака (1,2,3,4,5 и 6 правильных ответов), удовлетворительная и отличная — только один интервал. Это не значит, что величина «объема знаний» у ученика, получившего оценку 4, в два раза больше, чем у получившего оценку 2, а только показывает, что у первого ученика объем знаний больше, чем у второго. Насколько и во сколько раз больше, — этого сказать нельзя.

Поскольку ранговые числа являются порядковыми и ни в коей мере не характеризуют интервальных значений (для них интервалы условные, непостоянные значения), то над этими числами нельзя производить арифметические действия.

Основной областью, где широко применяется метод ранговой оценки, является исследование субъективных, нематериальных явлений учебного процесса и различных психических свойств и процессов, формируемых у учеников в ходе обучения и воспитания.

Необходимыми и достаточными условиями такого измерения являются:

1. Наличие точного критерия для установления наличия или отсутствия нужного признака у исследуемых объектов или явлений.

2. Наличие критерия для выявления количественных величин данного признака у исследуемых объектов или явлений.

Последний критерий должен дать исследователю возможность хотя бы приближенно оценить величину изучаемого признака (по формуле «больше-меньше»), т.е. установить, одинаково или не одинаково развит у этих объектов данный признак. Эти два условия позволяют исследователю не только отличить объекты с данным признаком от объектов, не обладающих этим признаком, например, успевающих от неуспевающих учеников (как в методе регистрации), но также установить, у кого какие успехи по формуле «выше-ниже», «больше-меньше» (второе условие).

ГРАФИЧЕСКИЙ МЕТОД ОБРАБОТКИ СТАТИСТИЧЕСКИХ ДАННЫХ

Какова же роль графического метода в статистическом анализе, какие преимущества дает он в сравнении с традиционным табличным методом?

Познавательная ценность статистических графиков объясняется их способностью отображать реальную действительность в простом, ясном и наглядном виде. Визуальная интерпретация объективных статистических показателей позволяет облегчить познание предмета исследования, делает его более осязаемым. Т.о., статистические графики могут дать новое знание о предмете исследования, которое в исходном цифровом материале непосредственно не проявляется. Выявление закономерностей, присущих тем или иным явлениям, факторов, их определяющих, дифференциация этих явлений во времени и пространстве — задачи, эффективно решаемые с использованием графического метода.

П.1 Основные элементы графика. Правила построения статистических графиков

Рассмотрим основные элементы статистического графика.

Поле графика — пространство, где расположены геометрические знаки, образующие график. Полехарактеризуется его форматом, т.е. размером и пропорциями (соотношением сторон).

Размер графика выбирается в соответствии с его назначением (демонстрация в аудитории, иллюстрация в статье, дипломной работе и т.д.).

Пропорции графика определяются законами геометрической гармонии и требованием обеспечения неискаженного зрительного восприятия графического образа. Неудобны для восприятия графики сильно удлиненной формы (как в вертикальном, так и в горизонтальном направлениях).

Геометрические знаки – знаки-символы, изображающие статистические величины, составляющие графический образ. Это -точки, прямые и кривые линии и их отрезки, части плоскости (круги, прямоугольники, квадраты), объемные фигуры (кубы, параллелепипеды, шары), негеометрические фигуры (знаки-символы, изображения предметов).

Выбор вида геометрических знаков определяется характером исходной информации (счетные множества- точки, динамика явлений — линейные графики, сравнение абсолютных и относительных величин- плоскостные и объемные фигуры и т.д.), а также основной целью, заложенной в данный график .

Пространственные ориентиры задаются координатной сеткой (диаграммы) или контурными линиями (картограммы).

Координатная сетка образуется пересечением линий, проходящих через деления вертикальной и горизонтальной шкал. Наиболее часто применяемая система координат — декартовая (прямоугольная), реже — полярная (круговые графики).

На горизонтальной шкале прямоугольных диаграмм обычно размещают независимые переменные (в т.ч. время), на вертикальной — зависимые переменные.

Основная горизонтальная (нулевая) линия обязательно должна быть показана на графике (координатные оси для координатных графиков и «платформа» для столбиковых диаграмм) и для наглядности выделена толщиной. Если уровни изображаемых показателей таковы, что основная часть координатной сетки остается неиспользованной, то на шкале делается разрыв (≀≀,≈), исключающий ненужную часть сетки, но с обязательным указанием нулевой линии. Невключение нуля в вертикальную шкалу является распространенной ошибкой, искажающей изображение, что может привести к неправильному выводу.

Масштабные ориентиры задаются масштабными шкалами (в координатных графиках) или масштабными знаками (в картограммах).

При выборе масштаба на вертикальной и горизонтальной шкалах следует добиваться правильной пропорции, соотношения между ними. Чрезмерное укорочение или удлинение вертикальной или горизонтальной шкалы также искажает изображение и может привести к неправильному выводу. Получение оптимальной пропорции достигается подбором (пробное построение нескольких вариантов) или опытностью составителя диаграммы.

Виды масштабных шкал: непрерывные и прерывные. Непрерывная шкала применяется для непрерывно меняющихся величин (всем точкам шкалы соответствует какое-либо число, а все промежуточные значения могут быть интерпретированы).

Прерывная (порядковая) шкала — шкала с величинами, промежуточные значения которой не интерпретируются. Так, например, если деления шкалы представлены помесячными данными — январь, февраль и т.д., то точка между январем и февралем ничего не обозначает, т.к. масштаб не предполагал дневных данных. В этих случаях графическое изображение не непрерывно. Оно представляет собой, как правило, отдельные точки и их нельзя соединять непрерывной линией. В дипломных работах часто встречаются ошибки такого рода.

Экспликация состоит из названия графика и объяснения знаков-символов. Название графика должно быть лаконичным и ясным, отвечающим на три основных вопроса: что, где, когда. Пояснения к вертикальным и горизонтальным шкалам должны раскрыть содержание отображаемых показателей, единицы их измерения.

П.2 Композиция статистического графика.

Под композицией графика понимается сочетание всех его элементов. Правильная композиция предполагает:

— тщательно продуманный отбор из имеющегося цифрового статистического материала тех данных, которые будут изображены на графике (таким образом, далеко не все полученные данные следует изображать графически);

— выбор формата (размера и пропорций) графика;

— выбор вида графика — того, который по мнению исследователя наиболее ярко отражает полученные данные;

— подбор масштаба (масштабных шкал и знаков);

— правильное расположение и сочетание всех элементов графика.

Создание правильной композиции должно преследовать главную цель — получить компактное простое и логичное изображение описываемого явления, дающее цельное представление о нем и, в то же время, подчеркивающее при необходимости те или иные особенности этого явления (состав, структуру, дифференциацию, динамику и т.п.).

Немаловажной задачей композиции графика является художественная, эстетическая сторона его оформления. График должен привлекать внимание, обеспечивая в то же время легкость его прочтения и усвоения.

Чтобы композиция графика отвечала отмеченным требованиям, следует при построении графиков соблюдать определенные правила.

П.3 Основные правила построения графиков.

1.Название графика должно быть ясным и полным, отражающим содержание и имеющим при необходимости особые пояснения.

2.Масштаб на горизонтальной и вертикальной шкалах должен быть оптимальным, не искажающим реальные соотношения анализируемых явлений.

3.Надписи и цифры располагаются, как правило, в нижней или правой части диаграммы.

4.Основной ряд полученных диаграмм следует располагать слева направо. Горизонтальную шкалу (по оси абсцисс) строить слева направо, вертикальную (по оси ординат)- снизу вверх.

5.Цифры шкалы следует наносить слева и снизу или вдоль осей.

6.Полезно включать в диаграммы числовые значения, соответствующие отдельным точкам кривой или математическую формулу кривой.

7.Если числовые данные не включены в диаграммы, желательно их дать рядом в табличной форме.

8.Нулевые линии (как вертикальную, так и горизонтальную) рекомендуется выделять на чертеже отдельно от всех других линий координатной сетки. Если по характеру данных это неудобно, то нужно показать нулевую линию посредством «разрыва» диаграммы.

9.Густота координатной сетки должна быть оптимальной, не затрудняющей чтения диаграммы.

10.Линии на диаграмме следует выделять от линий координатной сетки (толщиной или цветом).

Т.о. самая заметная линия- это линия самой диаграммы, немного тоньше — нулевая линия и самые незаметные- линии координатной сетки.

11.Если графики отражают серию наблюдений, рекомендуется ясно обозначать все точки, соответствующие отдельным наблюдениям.

12.Во всех случаях, когда это возможно, сравниваемые величины изображаются с помощью линий или полос и столбиков одинаковой ширины, но не площадей или объемов.

П.4 Виды и формы (классификация) графических изображений. Техника построения и анализа различных статистических графиков.

На протяжении развития графического метода разработано большое число видов и форм графических изображений. Этот процесс продолжается и поныне. В зависимости от целей и назначения, характера применяемых графических образов различают несколько видов графиков.

1.Показательные графики или сравнительные диаграммы: диаграммы простого сопоставления; диаграммы структуры; графики динамических рядов; изобразительные диаграммы.

2.Аналитические графики математической статистики: кривые и поверхности распределения (огивы, кумулянты, полигоны и гистограммы); выравнивающие и интерполяционные кривые; кривые эмпирических закономерностей.

3.Статистические карты: картограммы, картодиаграммы.

В свою очередь, эти основные виды графиков имеют многообразие подвидов и форм в зависимости от способа построения, вида масштабных шкал и знаков, графических форм и образов.

Рассмотрим подробнее только некоторые из видов статистических графиков, которые чаще всего используются при изображении данных, полученных в ходе психолого-педагогических исследований.

П.5 Показательные графики и сравнительные диаграммы.

Наиболее широко известны и часто применяются линейные графики, линейные, столбиковые, круговые (секторные) и векторные диаграммы.

При помощи линейного графика можно передать изменения какого-либо признака рядом чисел. Для сравнения двух или нескольких рядов чисел они обычно наносятся на одни и те же оси координат.

Рассмотрим конкретный пример, типичный для психолого–педагогических исследований. Предположим, что для проверки эффективности предлагаемого метода в двух классах — контрольном и экспериментальном- был проведен контрольный срез. Детям предложили решить 15 заданий. На рисунке 1 изобразим график, показывающий количество учащихся (в %) в контрольном и экспериментальном классах, давших верные ответы на различные виды заданий.

Соответствующий линейный график имеет вид:

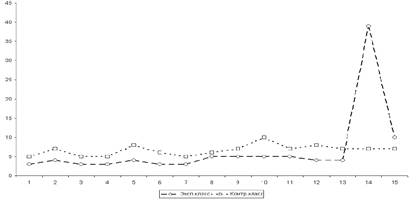
Рис.1 Сравнительная линейная диаграмма количества учащихся, давших верные ответы на задания.

На приведенном здесь графике по оси х откладывали число заданий, по оси у – процент правильных ответов. Сравнительный анализ этих графиков позволяет выявить ряд особенностей усвоения учащимися материала: данные кривые распределения свидетельствуют о неоднородности состава учащихся этих групп; в целом, кривая распределения экспериментального класса расположена под кривой распределения контрольного класса и только поднимается при значениях х =14 и х=15, причем весьма значительно (это значит, что большинство детей экспериментального класса решили по 14 или 15 заданий).

Таким образом, это свидетельствует о том, что использование экспериментальной методики дает более высокие результаты.

Данные исследования можно изобразить в виде линейной диаграммы.

Допустим, в результате проведения серии контрольных работ получены следующие данные:

Таблица 5.

Номер контрольной работы
Справились с заданиями (в %)

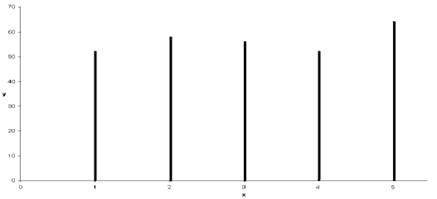
Рис. 2 Линейная диаграмма результатов серии контрольных работ.

На рисунке 2 дана линейная диаграмма качества знаний учащихся. По оси х откладываем номера контрольных работ, по оси у — количество детей, справившихся с данной контрольной работой ( в %).

Большую помощь подобные графики могут оказать в выявлении типовых ошибок. Для этого по оси абсцисс откладываются номера заданий, а по оси ординат — процент учащихся, допустивших ошибки в ответах на эти задания (или наоборот — давших правильные ответы).

Для большей наглядности эти данные можно соединить ломаной линией, хотя следует помнить, что промежуточные данные при этом истолковать никак нельзя (рисунок 3).

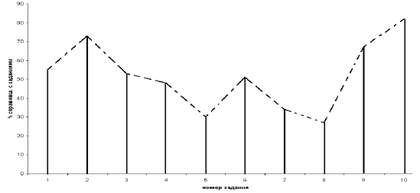
Рис.3. Диаграмма результатов выполнения заданий контрольной работы

Здесь показаны данные о проценте детей, давших верные ответы на задания.

Из этого графика видно, что дети успешнее всего справились с заданиями 2,9 и 10 (относительные максимумы диаграммы), а наиболее трудными оказались для обучаемых задания 5,7 и 8 (относительные минимумы диаграммы).

Именно их и следует проанализировать.

Линейная диаграмма очень наглядна и для сравнения результатов по двум вариантам тестов, если перед нами задача проверки их идентичности (т.е. включение равнотрудных заданий в тот и другой варианты).

В этом случае, данные числа ошибок по каждому типу заданий должны быть близкими. Рассмотрим рисунок 4.

По оси абсцисс отложим номера заданий, по оси ординат — % ошибочных ответов. В случае же резкого расхождения ломаных линий над каким-либо номером задания мы имеем несовпадение заданий данного типа по трудности. Эти задания следует либо изменить, либо исключить из теста.

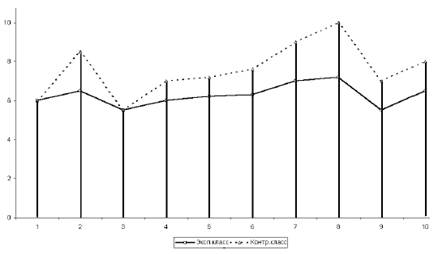
Рис.4. Сравнительная линейная диаграмма результатов контрольного среза.

Диаграммы в виде горизонтальных полос или вертикальных столбиков — наиболее простой и достаточно эффективный для анализа вид графических изображений. Применяются достаточно часто в психолого-педагогических исследованиях для сравнения уровней показателей по различным единицам, группам, для анализа состава и структуры по ряду объектов и в динамике.

Основа сравнения в полосовых и столбиковых диаграммах — линейная (одномерная).

Длины полос (высоты столбиков) или их составляющих пропорциональны величине изображаемых показателей. Ширина же полос и столбиков и промежутков между ними не имеет специального значения (произвольная), но должна быть одинаковой в пределах одной диаграммы. Обычно придерживаются правила, чтобы ширина промежутков была вдвое больше ширины самих полос. Рекомендуется включение в диаграмму масштабной шкалы.

Рассмотрим пример построения столбиковой диаграммы. Детям экспериментального класса предлагалось назвать любимые школьные предметы (допускалась возможность неоднозначного ответа).

Результаты опроса следующие:

Предмет	Математика	Природоведение	Русский язык	Физкультура
% детей, указавших данный предмет

В этом случае столбиковая диаграмма имеет следующий вид:

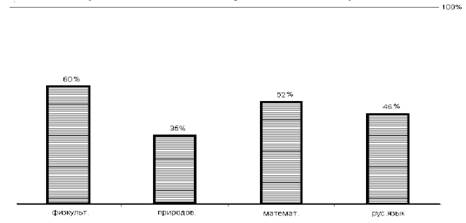
Рис.5. Столбиковая диаграмма, отражающая предпочтения детей в плане школьных предметов.

Рассмотрим еще один вид часто встречающихся графических изображений.

Круговые диаграммы эффективнее применять для анализа состава или структуры явлений. При этом, составные части целого изображаются секторами окружности соответствующей угловой величины (1% удельного веса принимается за 3,6 градуса длины окружности).

Техника построения секторных круговых диаграмм предполагает соблюдение следующих рекомендаций. Последовательность размещения секторов определяется их величиной: самый крупный помещается сверху, справа от вертикальной оси симметрии круга, а остальные — по движению часовой стрелки в порядке уменьшения их угловой величины. Каждый сектор должен иметь четкое обозначение на экспликации. Допускается указание цифр в пределах секторов или вне окружности. При малом угле сектора экспликация к нему указывается стрелкой.

Рассмотрим пример построения круговой диаграммы. Представим с помощью нее успеваемость учащихся параллели по конкретному предмету. Пусть оценку «5» по данному предмету имеют 15% учащихся, оценку «4»- 38% учащихся, «3»- 44% и оценку «2»- 3%. Подсчитаем угловые величины соответствующих секторов:

L5=(360°·15)/100=54° ; L4=(360°·38)/100=136.8°≈137°

L3=(360°·44)/100=158.4°≈158°; L2=(360°·3)/100=10.8°≈11°.

Теперь можно изображать соответствующую круговую диаграмму:

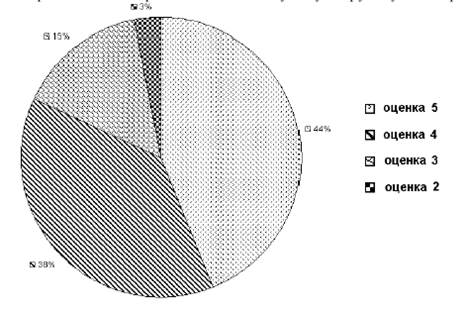
Рис.6. Круговая диаграмма успеваемости по данному предмету.

Круговые диаграммы могут иметь различный вид. Например, в исследовании Г.В. Ивановой, когда проверялась эффективность тестового контроля знаний, учитывались дифференцированно результаты тестов по проверке различных видов языковых знаний (тесты группы А — лексики, В — правил произношения, С — орфографии и т.д.).

Поэтому круг был разделен на секторы пропорционально тем долям, которые приходились на каждый вид тестов (А-25%, В-20%, С-20%, D-32%, E-3%).

Внутри же каждого сектора заштриховывался процент учеников, давших неправильные ответы. В этом случае сам сектор принимался за 100%. Такого типа круговая диаграмма несет в себе очень большой информационный потенциал. Вместо того, чтобы рисовать пять отдельных круговых диаграмм, изображается только лишь одна.

Круговая диаграмма имеет такой вид:

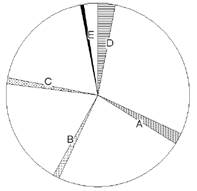
Рис.7. Круговая диаграмма результатов тестового контроля знаний.

Сравнительные диаграммы объединяют большую группу графиков, решающих задачи представления результатов статистического наблюдения в сопоставимом виде и дающих возможность сравнения изучаемых явлений в том или ином аспекте — по величине, структуре, территории, в динамике и т.д. Очень часто сравнительные диаграммы используются студентами при написании дипломных работ при сопоставлении либо результатов констатирующего и контрольного срезов в одном классе, либо при сравнении результатов одного и того же среза, но в контрольном и экспериментальном классах. Важно помнить, что данные, изображаемые на сравнительных диаграммах должны быть сопоставимы.

Рассмотрим пример. Изобразим результаты констатирующего и контрольного экспериментов в экспериментальном классе. Для замера уровня знаний по данной теме детям предлагались задания трех типов. В таблицу занесены сведения о проценте детей, справившихся с заданиями:

Эксперимент	I тип	II тип	III тип
Констатирующий	40%	50%	56%
Контрольный	45%	67%	76%

А теперь изобразим эти данные:

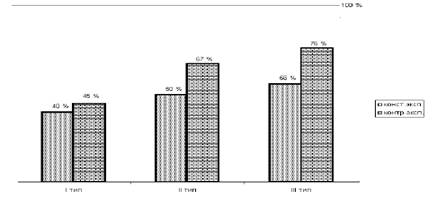
Рис.8. Сравнительная диаграмма результатов двух экспериментов

Наиболее распространенным видом сравнительных диаграмм являются арифметические линейные диаграммы, используемые, главным образом, для характеристики динамических рядов и рядов распределений, состоящих из большого количества исследующихся величин.

В ряде случаев, когда необходимо показать динамику интересующего нас показателя в отношении отдельных учащихся используют векторные диаграммы. Особенно целесообразно построение векторных диаграмм, когда в эксперименте участвует небольшое количество детей и для исследователя интересен вопрос о динамике прогресса каждого ребенка, принимающего участие в эксперименте.

Рассмотрим пример построения такой диаграммы. В ходе констатирующего и контрольного обследования учеников некоторого класса получены ранговые данные, свидетельствующие об уровне сформированности некоторого приема. Данные представлены в таблице:

N фамилии
Ранг (конст.эксп.)
Ранг (контр.эксп.)

Покажем на векторной диаграмме изменения количественного значения ранга для каждого ребенка.

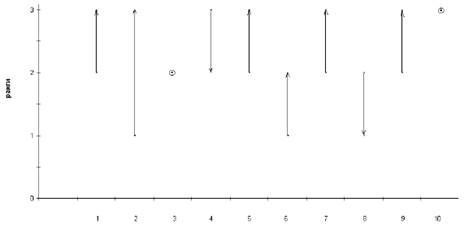
Рис.9. Векторная диаграмма ранговых показателей учащихся …класса.

П.6 Аналитические графики математической статистики.

Полигон и гистограмма.

Полигон и гистограмма — это графические изображения результатов статистического исследования. Они относятся к аналитическим кривым математической статистики. Здесь и далее мы рассмотрим, как изображаются количественные данные, полученные в ходе статистических исследований. Полигон строится в тех случаях, когда распределение изучаемого признака — точечное.

О п р е д е л е н и е. Полигон— это статистическая аналитическая кривая, для построения которой необходимо по оси абсцисс отложить значения вариант хi , а по оси ординат — соответствующие им относительные частоты. Полученные точки с координатами (хi,рi) соединяют отрезками.

При построении полигона необходимо всегда доводить линии справа и слева до нулевых значений относительных частот, т.е. указывать такие значения вариант, которые в выборочной совокупности не встречались.

П р и м е р 2. Пусть дано статистическое распределение.

Xi	1.5	3.5	5.5	7.5
Ni
Pi	0.1	0.2	0.4	0.3

Построим полигон частот: по оси абсцисс отложим значения вариант, а по оси ординат — относительные частоты. Изобразим полученные точки, а затем их соединим:

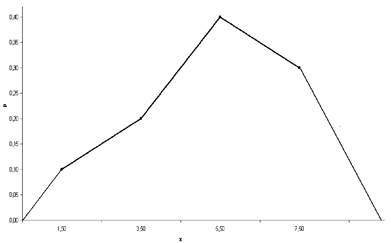
Рис.10. Полигон распределения относительных частот

По изображению полигона можно наглядно судить о том, какое значение признака наиболее популярно, а также, насколько это значение «популярнее», чем все остальные значения вариант. Также, по виду полигона, можно судить о том, каков характер распределения изучаемого признака ( близок ли он к нормальному или нет).

В случае, когда изучаемый признак имеет интервальное распределение, вместо полигона строится гистограмма по следующему правилу.

О п р е д е л е н и е . Гистограмма— это графическое изображение статистических данных, для построения которого по оси абсцисс откладываются интервалы, а затем над каждым интервалом строится прямоугольник, площадь которого равна численности данного интервала.

Очевидно, что самый высокий прямоугольник будет построен над интервалом, в котором сосредоточено большинство вариант.

Проиллюстрируем понятие гистограмма построением данного графического изображения для исследования, результаты которого представлены в таблице 3. Рекомендуется перед построением гистограммы вычислить высоту каждого прямоугольника, беря во внимание длину интервалов.

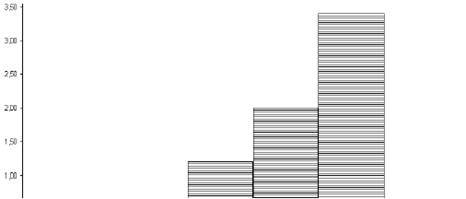
Рис.11. Гистограмма распределения количества набранных баллов в результате выборочного тестового обследования.

Кумулятивный ряд. Кумулянта и огива.

О п р е д е л е н и е. Накопленной частостью (частотой) в точке х называют суммарную частоту (частость) членов генеральной совокупности со значением признака меньшим, чем х.

Если в статистическом ряду вместо относительных частот записать соответственно накопленные частоты, то получим кумулятивный ряд. Для графического изображения кумулятивных рядов используют кумулянты и огивы.

О п р е д е л е н и е . Кумулянта – это аналитическая кривая математической статистики, для построения которой по оси абсцисс отмечаются точки, соответствующие границам интервалов или значениям признака, в каждой такой точке восстанавливается перпендикуляр, длина которого пропорциональна накопленной частости и концы соседних перпендикуляров соединяют отрезками.

Если по горизонтальной оси откладывать накопленные частости, а по вертикальной- значения признака, то полученная ломаная называется огива.

П р и м е р 3. Предположим проведено 1000 испытаний на предмет наличия или отсутствия интересующего нас признака. Полученные результаты были занесены в таблицу:

Знач. Вар.	180-190	190-200	200-210	210-220	220-230	230-240	240-250
Числ.

Построим кумулятивный ряд и начертим кумулянту и огиву.

Р е ш е н и е. Найдем накопленные частоты:

w(190)=50, w(200)=50+90=140, w(210)=290, w(220) =570, w(230) =790, w(240) =910, w(250) =1000.

Следовательно, кумулятивный ряд для данной задачи имеет вид:

Знач. Вар.	180-190	190-200	200-210	210-220	220-230	230-240	240-250
Нак.част.

На основе полученных данных начертим кумулянту:

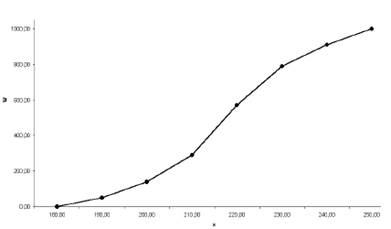
Рис.12. Кумулянта накопленных частот при исследовании признака

Графическое оформление результатов, тем не менее, не должно быть самоцелью. Это лишь средство более наглядного представления связей и зависимостей в изучаемых явлениях, и поэтому они всегда должны служить подспорьем в проведении качественного и количественного анализа собранного массового материала. Выбор того или иного вида графиков или диаграмм целиком определяется целью и задачами эксперимента и характером собранных экспериментатором данных. Здесь приведены лишь наиболее распространенные способы графического оформления.

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СОВОКУПНОСТИ

Математические методы уже находили применение в описанных выше приемах и способах анализа и обработки массового материала. Это были и общий подсчет результатов ответов, и вычисление процента давших правильные и неправильные ответы, и расчет угловых величин секторов для круговых диаграмм и т.д. Остановимся специально на вопросе о применении статистических методов для обработки результатов педагогического эксперимента.

В настоящее время для анализа результатов педагогического эксперимента широко используются методы математической статистики. В педагогической литературе предлагается ряд методик статистической обработки данных педагогического эксперимента (Л.Б.Ительсон, Ю.В.Павлов и др.).

При использовании методов математической статистики следует иметь в виду, что сама статистика не раскрывает сущности явления и не может объяснить причины возникающих различий между отдельными сторонами явления. Например, анализ результатов проведенного исследования показал, что используемый метод обучения дал более высокие результаты по сравнению с ранее зафиксированными. Однако данные вычисления не могут дать ответ на вопрос, почему новый метод лучше прежнего.

Статистические методы в педагогике используются лишь для количественной характеристики явлений. Для того, чтобы сделать выводы и заключения, необходим качественный анализ. Таким образом, в педагогических исследованиях методы математической статистики следует использовать осторожно, учитывая особенности педагогических явлений.

Так, большинство числовых характеристик в математической статистике применяются в том случае, когда изучаемое свойство или явление имеет нормальное распределение, которое характеризуется симметричным расположением значений элементов совокупности относительно средней величины. . К сожалению, в виду недостаточной изученности педагогических явлений, законы распределения по отношению к ним, как правило, неизвестны. Далее, для оценки результатов исследования часто берут ранговые величины, которые не являются результатами количественных измерений. Поэтому с ними, как указывалось ранее, нельзя производить арифметические действия, а значит и вычислять для них числовые характеристики.

Каждый статистический ряд и его графическое изображение представляют собой сгруппированный и наглядно представленный материал, который следует подвергнуть статистической обработке.

Статистические методы обработки позволяют получить ряд числовых характеристик, позволяющих сделать прогноз развития интересующего нас процесса. Эти характеристики, в частности, позволяют сравнивать разные ряды чисел, полученные при педагогических исследованиях, и делать соответствующие педагогические выводы и рекомендации.

Все вариационные ряды могут различаться друг от друга следующими признаками:

1. Размахом, т.е. верхней и нижней его границами, которые обычно называют лимитами.

2. Значением признака, вокруг которого концентрируется большинство вариант. Это значение признака отражает центральную тенденцию ряда, т.е. типичное для ряда.

3. Вариации вокруг центральной тенденции ряда.

В соответствии с этим, все статистические показатели вариационного ряда подразделяются на две группы:

-показатели, которые характеризуют центральную тенденцию или уровень ряда;

— -показатели, характеризующие уровень вариации вокруг центральной тенденции.

— К первой группе относятся различные характеристики средней величины: мода, медиана, средняя арифметическая, средняя геометрическая. Ко второй — вариационный размах (лимиты), среднее абсолютное отклонение, среднее квадратичное отклонение, дисперсия, коэффициенты асимметрии и вариации. Существуют и другие показатели, но мы их рассматривать не будем, т.к. они пока не применяются в педагогической статистике.

—

ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ ЦЕНТРАЛЬНУЮ ТЕНДЕНЦИЮ РЯДА

Обычно в педагогике понятие среднего не связывают с определенным числом, хотя используют его довольно часто. Например, средняя успеваемость, средний ученик и т.д. Вместе с тем, вычисление средних математических величин – математического ожидания, моды и медианы — может дать определенную числовую характеристику наблюдаемого свойства, явления и позволяет сравнить числовые характеристики исследуемых различий.

П. 1 Вычисление математического ожидания выборки.

Математическое ожидание или среднее арифметическое значение выборки — одна из основных числовых характеристик, показывающая центральную тенденцию ряда. При составлении прогноза развития интересующего нас процесса эта характеристика является базовой. Вместе с тем, при сопоставлении различных исследований, она позволяет объективно оценить различия между ними. Показатель «математическое ожидание» может быть использован при определении среднего количества решенных задач, допущенных ошибок, усвоенных единиц знаний и т.д., т.е. тех характеристик педагогических явлений, которые носят количественный характер.

Пусть интересующий нас признак имеет точечное распределение.

О п р е д е л е н и е. Математическим ожиданием выборки называется сумма произведений всех ее возможных значений на соответствующие относительные частоты:

М(Х)=х1р1+х2 р2+…+хк рк, где рк =ni/n, I=1,…,k.

Т.е. математическое ожидание — это «среднее взвешенное» возможных значений.

П р и м е р 4. Найти математическое ожидание для следующих данных:

Варианта
Частота
Относительная частота	1/20	5/20	7/20	3/20	4/20

В этом случае: М(Х)=2· 1/20+ 6· 5/20+10· 7/20+12· 3/20+ 14 ·4/20=9.7

По сути, как было подчеркнуто выше, математическое ожидание — это ни что иное, как среднее арифметическое наблюдаемых значений интересующего нас признака (в этом нетрудно убедиться).

Смысл (интерпретация) математического ожидания состоит в том, что оно заменяет все значения совокупности чисел. Иными словами, если взамен каждого значения ряда взять математическое ожидание, то мы при этом обеспечим минимальную ошибку отклонений от среднего.

А теперь обратимся к случаю, когда изучаемый признак имеет интервальное распределение. Пусть интервалы имеют длину h. Введем номера этих интервалов в порядке возрастания их величины, поместив начало отсчета вблизи от середины опытных данных и одновременно стремясь поместить его в интервал, соответствующий максимальной численности. Будем считать, что все наблюдения, попавшие в данный отрезок длины h, имеют значение, равное средней абсциссе этого отрезка.

Предположим, что для нулевого интервала это значение равно zо .Тогда для отрезка с номером k среднее значение равно zк = zо +kh.

Если в отрезок с условной вариантой zк попало nк наблюдений, а всего наблюдений было n, то среднее их значение равно

М(Х)=1/n Σ nk zk =1/n Σ (zo +kh)nk =zo +h/n Σ knk =zo +kh ,

где k=1/n Σ knk . Здесь и далее суммирование по k.

П р и м е р 5. Вычислим математическое ожидание для признака, имеющего интервальное распределение. Данные возьмем те, которые были приведены в § 7 (таблица 3).

Расширим таблицу, введя дополнительные строчки, так, как было указано выше:

Интервалы (классы)	20-25	25-30	30-35	35-40	40-45	45-50
ni							S = 40
ki	-4	-3	-2	-1
niki	-8	-9	-12	-10			S = -37

Тогда математическое ожидание равно: М(Х)= 42,5+ 5·(-37)/40≈37,9.

П.2 Мода и медиана.

Следующая средняя величина — мода. Ею пользуются в тех случаях, когда хотят охарактеризовать явление на основе значения признака, встречающегося чаще всего.

О п р е д е л е н и е. Мода – это наиболее часто встречающееся значение признака.

Необходимо подчеркнуть, что мода представляет собой наиболее частое значение признака, а не частоту этого значения.

Рассмотрим случай точечного распределения. В совокупности оценок успеваемости 2,3,4,4,4,5,5 модой является оценка 4, потому, что эта оценка встречается чаще других. Принято считать, что в случае, когда все значения оценок встречаются одинаково часто, совокупность данных моды не имеет. Например, в совокупности 3,3,3,4,4,4,5,5,5 моды нет.

Если две несмежные оценки в совокупности имеют равные частоты и они больше частот других оценок, то существуют две моды. В примере совокупности 2, 3, 3, 4, 5, 5 модами являются оценки 3 и 5. В этом случае говорят, что совокупность оценок является бимодальной. Большие совокупности данных являются бимодальными, если они образуют полигон относительных частот с двумя вершинами, даже тогда, когда частоты не строго равны. В последнем случае различают большие и малые моды. Наибольшей модой в группе данных называют то значение варианты, которое чаще встречается, т.е. удовлетворяет определению моды. В практике встречаются большие совокупности, имеющие несколько малых мод. Это характерно для полигона с тремя и более вершинами.

Мода, как мера центральной тенденции, имеет следующую интерпретацию. Мода является такой характеристикой, т.е. имеет такое значение, которое наилучшим образом «заменяет все значения». Когда заменяют модой любое значение ряда чисел, мы имеем наибольшую частоту совпадений с числами ряда. Таким образом, мода тоже является характеристикой, на основе которой можно составлять прогноз развития интересующего нас процесса.

Следует заметить, что для малых групп часто о такой замене не может быть и речи. Например, группа из пяти учащихся имеет следующие оценки: 2,2,2,5,5. Модальное значение данной группы равно 2. Эта цифра точно характеризует успеваемость первых трех учеников, но является слишком некорректной для двух других.

Теперь рассмотрим другой случай. Пусть распределение интервальное. Как в этом случае вычисляется мода? Для начала следует найти модальный интервал, т.е. интервал, которому соответствует максимальная частота ns. Если Х’s — X»s -модальный интервал, а интервалы вариационного ряда имеют постоянную ширину h, то мода изучаемого признака вычисляется:

Мо Х=Х’s +h· (ns-ns-1)/(( ns-ns-1)+( ns-ns+1)),

где ns-1 , ns+1 — частоты, находящиеся в соответствии с интервалами, предшествующим модальному и следующим за ним.

П р и м е р 6. Данные статистического исследования представлены в таблице:

Количественное Значение признака	120-140	140-160	160-180	180-200	200-220	220-240	240-260	260-280
Число Случаев

Найти Мо Х-?

Р е ш е н и е.

Т.к. максимальная частота (n =58) соответствует интервалу 180-200, то Х’s=180, ns-1 =19, ns+1 =53. Значит,

Мo Х=180 + 20·(58-19)/(39+5)=197,73.

Еще одним показателем, характеризующим центральную тенденцию ряда, является медиана.

О п р е д е л е н и е. Медианой Ме Х называется значение признака, относительно которого генеральная совокупность делится на две равные по объему части, причем в одной из них содержатся члены, у которых значение признака не превосходит Ме Х, а в другой — не меньше Ме Х.

Очень часто результаты педагогических исследований выражаются в виде оценок успеваемости учащихся, которые являются результатом рангового измерения. Однако в этом случае нельзя пользоваться математическим ожиданием для вычисления центральной тенденции. Средняя успеваемость класса, вычисляемая как среднее арифметическое — бессмысленная величина, так как расстояние между 2 и 3 не равно расстоянию между 5 и 4. Оценки эти — показатели качества, а не количества измеряемого явления. Полученные оценки не обозначают величину, а показывают отношение одного значения признака к другому.

Для характеристики полученного ряда в статистике как раз и пользуются медианой.

П р и м е р 7. Пусть в результате выполнения работы в контрольном и экспериментальном классах получены следующие оценки:

Классы	Оценки
Контрольный
Экспериментальный

Расположим полученные ряды оценок по порядку от минимальных значений до максимальных:

Классы	Оценки
Контрольный	2222233333333333 33444444444445555
Экспериментальный	2233333333344444 44444444445555555

Теперь можно назвать медиану для каждого класса (значение ее выделено).

Но это очень приблизительное значение медианы. Для уточнения его следует использовать другой подход, аналогичный тому, который используется в случае интервального распределения.

Если распределение интервальное, то сначала надо найти медианный интервал X’p- X»p, интервал, в котором расположено значение признака, являющегося медианой. Тогда можно вычислить значение самой медианы по следующей формуле:

MеX = X’p +h· (n/2- w(X’p))/ np,

где h- ширина интервала, n- объем генеральной совокупности, w (Х’p)- накопленная частота до p-го интервала, np — частота p-го интервала, p- номер медианного интервала.

П р и м е р 8. Рассмотрим пример 6 и вычислим для данного вариационного ряда медиану. Для ее нахождения строим кумулятивный ряд:

xi	120-140	140-160	160-180	180-200	200-220	220-240	240-260	260-280
wi

Найдем номер медианного интервала s из условия:

w(X’p) < n/2, w(X»p) > n/2. Имеем n/2=180/2=90. Тогда w(X’4)=84 < 90, w(X’5)=137 > 90, следовательно,

Ме Х = 200 + 20·(90-84)/53 =202,26.

Вернемся к примеру 7. Ранее было отмечено, что полученные нами значения медиан весьма приблизительны. Вычислим их точнее. Как и в случае интервального распределения,

M еX = X’p +h· (n/2- w(X’p))/ np,

здесь X’p- начало класса, в котором находится медиана,

h- величина классового промежутка,

np- частота медианного класса, остальные обозначения имеют стандартное значение.

Найдем для каждого класса точное значение медианы.

Для контрольного: X’p = 3, h=1, n=33, w(X’p)=5, np=13. Значит,

Ме Х =3+1·(33/2-5)/13≈3,9.

Для экспериментального класса: X’p = 4, h=1, n=33, w(X’p)=11, np=15. Значит,

Ме Х =4+1·(33/2-11)/15≈4,37.

Таким образом, мы можем сказать, что средний уровень знаний учащихся в контрольном классе -3,9, а обучаемых в экспериментальном классе — 4,37.

Интерпретацию медианы, т.е. ее смысл, раскроем на следующем примере. Пусть имеем следующий ряд оценок 2 2 3 4 5 5 5. Для этого случая медиана равна 4. Разность между 4 и 2 составляет два, между 4 и 3 – один, между 4 и 5- один. Рассмотрим сумму этих разностей, взятых по модулю: 2+2+1+1+1+1=8. Эта сумма всегда будет меньше суммы разностей относительно любого другого числа данного ряда. Таким образом, медиана представляет собой такую точку на числовой оси, для которой сумма абсолютных разностей всех значений относительно медианы всегда меньше суммы разностей относительно любой другой точки. Иными словами, если вместо каждой оценки ряда выбрать медиану, то будет допущена минимальная суммарная ошибка.

Следует отметить, что каждая мера центральной тенденции числовых рядов обладает характеристиками, которые являются ценными в определенных условиях. Мода проще всего вычисляется, и для больших совокупностей она является достаточно стабильной мерой центра распределения. В малых совокупностях чисел мода, как правило, нестабильна. Например, для ряда чисел 333455 мода равна 3, но если одну из троек заменить 5, то мода станет уже равной пяти.

Медиана более стабильная числовая характеристика. На нее не влияют «большие» и «малые» варианты. Например, для больших совокупностей вариант медиана не изменится, если число максимальных или минимальных вариант резко изменится. Например, совокупности 22233334445555 и 33333334444445 имеют одинаковые медианы. А вот на величину математического ожидания влияет изменение каждого значения варианты. Для многих числовых совокупностей педагогических измерений мода близка к двум другим мерам — медиане и математическому ожиданию. Медиана занимает промежуточное положение между модой и математическим ожиданием.

Центральная тенденция совокупности данных с большими крайними выбросами наилучшим образом характеризуется медианой, когда гистограмма унимодальна. Например, достаточно одного большого крайнего значения, чтобы сместить математическое ожидание совокупности намного дальше, чем это характерно для данной выборки.

В симметричных унимодальных совокупностях математическое ожидание, мода и медиана совпадают, что соответствует нормальному распределению выборочных данных. Отсутствие симметрии в полигоне или гистограмме оказывает определенное влияние на соотношения между модой, медианой и математическим ожиданием. Если большинство оценок расположено слева от вершины полигона относительных частот, то математическое ожидание примет минимальное значение, мода — максимальное, а медиана — между ними. Если группа данных измерения выбрана из большой симметричной группы, то математическое ожидание выборки будет ближе к центру большой группы, чем медиана и мода.

Далее рассмотрим числовые характеристики выборочной совокупности, которые характеризуют вариации вокруг центральной тенденции. Их нахождение основывается на вычислении математического ожидания, которое, как отмечалось выше, имеет ограниченное применение и не подходит для вычисления по характеристикам успеваемости в баллах, а также для различных ранговых измерений.

ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ ВАРИАЦИИ ВОКРУГ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

В §10 указывалось, что к показателям, характеризующим вариации вокруг центральной тенденции, относятся размах вариации, дисперсия, среднеквадратичное отклонение от среднего и коэффициент вариации.

О п р е д е л е н и е. Дисперсия выборки («рассеивание»)- это величина, характеризующая разброс ее значений вокруг среднего. Обозначается Д(Х).

Чем больше дисперсия, тем «случайнее» изучаемый процесс. Дисперсия определяет степень правдоподобия прогноза развития изучаемого процесса. Рассмотрим пример. Допустим, вариационный ряд имеет следующий вид: 42635445362264435. Нетрудно убедиться, что математическое ожидание для этой выборки равно 4. Это значит, как указывалось выше, что варианта 4 отражает центральную тенденцию ряда, т.е. является типичной для него и поэтому, если пытаться оценить значение восемнадцатой варианты, самое вероятное значение- это 4. При этом следует помнить, что 100%-ых прогнозов не существует, а можно говорить лишь о более или менее вероятных значениях. Теперь рассмотрим другой вариационный ряд: 43553444355533435. И здесь математическое ожидание выборки равно 4, а значит, для прогноза значения восемнадцатой варианты тоже стоит выбрать 4. Возникает сразу ряд вопросов: в каком из этих двух случаев прогноз более состоятелен, т.е. в каком случае вероятность ошибиться меньше, с чем это связано? Забегая вперед, ответим. Во втором случае процесс менее случаен, у него суммарная степень отклонения вариант от математического ожидания меньше или, как говорят, меньше разброс. А значит, вероятность того, что значение восемнадцатой варианты равно 4, во втором случае выше, чем для первой выборки. То есть, для первой выборки значение дисперсии выше, чем для второй.

Рассмотрим, как вычисляется дисперсия.

Для точечного распределения

Д(Х)= (х1 — М(Х))² р1 + (х2 — М(Х))² р2 +…+(хn -М(Х))² рn ,

где хi- значения вариант, рi-значения соответствующих относительных частот.

Для примера 4 вычислим дисперсию. Напомним, что М(Х)=9.7. По формуле:

Д(Х)= (2-9.7)² ·1/20+ (6-9.7)² ·5/20+ (10-9.7)² ·7/20+ (12-9.7)² ·3/20+ (14-9.7)²·4/20=10.91.

С дисперсией связана другая характеристика- с р е д н е к в а д р а т и ч н о е о т к л о н е н и е (или стандарт):

σ² = Д(Х).

Если для некоторой выборки мы имеем М(Х) и σ, то имеем ориентировочное представление о том, в каких пределах могут лежать наиболее вероятные значения интересующего нас признака: [M(X)- σ, M(X)+σ].

Для примера 4 σ ≈3.3 и, значит, соответствующий интервал для выборки из примера 4 будет [6.4; 13]. Нетрудно видеть, что при большом значении дисперсии интервал прогноза будет большим, а значит, такой прогноз для исследователя не очень интересен, и он лишний раз свидетельствует о том, что интересующий процесс «весьма случаен».

Вычислим дисперсию в случае интервального распределения изучаемого признака. Каждый интервал мы заменяем его средним значением, а далее пользуемся формулой, которая использовалась для точечного распределения:

Д(Х) =1/n Σ (zк –М(Х))² nк =1/n Σ (zо +kh-zо —kh)² nk =h² /n Σ (k-k)² nk =

= h ²(1/n Σ k² n —к² ),

где k=1/n Σ knk и суммирование по k.

Проиллюстрируем описанные вычислительные процедуры, рассмотрев случай интервального распределения выборочных данных. Обратимся опять к примеру 5. Для упрощения вычислений дополним таблицу:

Итервалы (классы)	20-25	25-30	30-35	35-40	40-45	45-50
ni							S = 40
ki	-4	-3	-2	-1
niki	-8	-9	-12	-10			S=-37
niki²							S=95

Для данного примера

Д(Х)= 5²· (1/ 40·95- (37/40)²)≈37.98; σ ≈6.16.

Следующая характеристика, также свидетельствующая об уровне вариации вокруг центральной тенденции- размах вариации.

О п р е д е л е н и е. Размах вариации— это числовая характеристика, равная по величине разности между максимальным и минимальным значениями вариант:

V(Х)= хmax-хmin.

От величины размаха вариации зависит величина дисперсии. Чем больше размах вариации, тем больше будет значение дисперсии.

О п р е д е л е н и е . Коэффициент вариации— это числовая характеристика выборки, которая показывает соотношение между математическим ожиданием выборки и ее дисперсией:

R(Х)=М(Х)/Д(Х)·100%

ВЫВОДЫ ПО ЭКСПЕРИМЕНТУ

Одна из труднейших задач проведения эксперимента — подведение его итогов. Выводы по эксперименту, прежде всего, должны быть ориентированы на выдвинутую с самого начала гипотезу. Они должны подтверждать гипотезу или противоречить ей. В первом случае следует очень кратко воспроизвести основные данные, свидетельствующие в ее пользу, во втором случае — дать объяснение, попытаться выявить причину основных расхождений, и в случае принятия объективных данных, опровергающих гипотезу, изменить ее в соответствии с ними. Второе, что очень важно учесть при поведении итогов, — требование о том, чтобы выводы были соизмеримыми с экспериментальной базой и собранными данными, т.е., чтобы выводы не были «глобальными», выходящими за пределы поставленных задач и области конкретных исследований

Хотя исследователя важно предупредить о необходимости избегать развернутых выводов, тем не менее, нельзя не отметить, что при подлинно научной экспериментальной проверке какой-либо исследовательской проблемы с учетом связи ее с рядом других факторов, в эксперимент оказываются втянутыми и эти факторы, и ряд дополнительных связей. Поэтому данные и выводы по эксперименту в известной степени могут и должны затрагивать и их. Исследователь поэтому может высказать некоторые предположения о связи данной области с пограничными зонами, но все же больше он должен говорить о необходимости продолжения дальнейших исследований в этих областях с изучением дополнительных влияний или влияния тех факторов, которые были учтены еще в недостаточной мере. Делая выводы, исследователь должен еще раз оговорить условия эксперимента, которые могли повлиять на степень надежности тех данных, по которым делаются выводы, и подчеркнуть, что эксперимент не универсальный и не единственный метод, которым следует пользоваться для разработки данного аспекта, и дать оценку его роли и места в системе других методов, использовавшихся им при ведении исследований по проблеме. Если результаты эксперимента ( и данные, полученные с помощью других методов ведения исследования) свидетельствуют о том, что следует ставить вопрос о необходимости внедрения тех или иных проверявшихся средств, методов и приемов обучения, исследователь, завершая свое исследование, может наметить некоторые пути осуществления этого внедрения.

Таким образом, заключительный этап обработки данных эксперимента включает:

1. Соотнесение выводов с общей и частной гипотезой.

2. Четкое ограничение области, на которую могут быть распространены полученные выводы.

3. Высказывание предположений о возможности их распространения на некоторые пограничные области и указание основных направлений дальнейших исследований в этой и смежной областях.

4. Оценку степени важности выводов в зависимости от чистоты условий эксперимента.

5. Оценку роли и места эксперимента в системе других применявшихся в данном исследовании методов.

6. Практические предположения о внедрении в практику результатов проведенного исследования.

ЛИТЕРАТУРА

1.Белова А. Математическая статистика, Москва,1976

2.Вентцель Е.С. Теория вероятностей, Москва,1977

3.Гмурман В.Е. Теория вероятностей и математическая статистика, Москва, Изд-во «Высшая школа»,1977

4.Факультативный курс по основам теории вероятностей и математической статистике, Москва,1986

5.Завадский Ю.В. Основные сведения по математической статистике. — Курс лекций,Москва,1971

6.Лихолетов И.И. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике, Минск,1976.

Примеры похожих учебных работ

Анализ педагогических условий социальной работы по их генезу

Структура и содержание анализа педагогических условий социальной работы по их генезу Заключение Список ... отсутствие навыков поведения в определенной ситуации и т.д. Признаки дезадаптивного состояния проявляются первоначально в том, что возникают ...

Социальное обеспечение безработных граждан. Психолого — педагогическая помощь ...

... ст. 3) — это сложное социально-экономическое явление, не позволяющее части экономически активного населения, желающего работать ... данные клиента, его профессия и причины обращения в службу занятости. Регистрация в целях поиска подходящей работы. ...

Глава 7. Педагогические основы социальной работы

... микрогруппы, коллектива в целом. Справедливая оценка, принятая человеком, помогает ему наметить новые цели в его самосовершенствовании. Необходимой частью педагогической подсистемы социальной работы являются методы закрепления положительного опыта ...

Психолого-педагогические условия эффективности работы социального педагога с детьми ...

... Общая проблема особенностей социально-педагогической работы в учреждениях интернатного ... важность, именно поэтому существенное значение здесь приобретает роль педагога ... девиантному поведению [11]. По данным Государственного комитета статистики Украины, ...

14. Педагогические аспекты социальной работы

... его социализации. Функции и прикладные задачи педагогической деятельности в социальной работе. диагностическая функция.с диагностической функцией связаны проблемы оценки многих основных свойств социальной работы: включённость индивидуумов и групп ...

Педагогические основы социальной работы

... четко разграничивать социально-педагогическую деятельность как официально ... как происходит расширение их семантических значений и образование новых грамматических ... её постоянной "работой" по спасению своей ... милосердия раскрывает в данных подходах его ...

ОБЩИЕ И СПЕЦИАЛЬНЫЕ МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЙ

Оглавление

Методы психолого-педагогического исследования; Теоретические методы исследования

ВВЕДЕНИЕ

Методы эмпирического педагогического исследования: наблюдение

ОБЩИЕ И СПЕЦИАЛЬНЫЕ МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

изучение методов диагностики и коррекции развития графомоторных ...

Педагогическая психология 10

Темы курсовых работ по дисциплине «Социальная психология малых групп»

СУЩНОСТЬ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ПЕДАГОГИЧЕСКИХ ЯВЛЕНИЙ

МЕТОДИКА РАЗРАБОТКИ ПРОГРАММЫ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА

МЕТОДИКА АНАЛИЗА ДАННЫХ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА

ОСНОВНЫЕ МЕТОДЫ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ПЕДАГОГИЧЕСКИХ ЯВЛЕНИЙ

Необходимыми и достаточными условиями такого измерения являются:

ГРАФИЧЕСКИЙ МЕТОД ОБРАБОТКИ СТАТИСТИЧЕСКИХ ДАННЫХ

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СОВОКУПНОСТИ

ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ ЦЕНТРАЛЬНУЮ ТЕНДЕНЦИЮ РЯДА

ПОКАЗАТЕЛИ, ХАРАКТЕРИЗУЮЩИЕ ВАРИАЦИИ ВОКРУГ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

ВЫВОДЫ ПО ЭКСПЕРИМЕНТУ

ЛИТЕРАТУРА